“5E”模式下数学命题教学中的“问题链”设计

——以“直线与平面垂直判定定理”为例

打开文本图片集

中图分类号：G632 文献标识码：A文章编号：1008-0333（2025）30-0011 -04

抽象、推理与模型是三大数学基本思想，其中逻辑推理的数学素养体现了数学的基本特征之一-严谨性[1].数学命题的教学是培养学生逻辑推理核心素养的关键途径，通过设计层层递进、相互关联的数学问题链，可引导学生经历数学命题的探究与发现过程，积累逻辑推理的数学经验，提升学生的自主思考能力.然而，在中学数学教学实践中，教师频繁提问却往往遭遇学生的沉默，这种现象表明问题设计的合理性亟须提升.如何有效运用“问题链”教学法，激发学生思考并促进其积极参与课堂活动，已成为亟待解决的关键问题

“5E"教学模式由引入（Engagement）、探究（Ex-ploration）、解释（Explanation）、拓展（Elaboration）和评估（Evaluation）五个阶段构成[2]，在该模式下，“问题链”成为引领学生进行知识探索和认知构建的关键线索.本文以“直线与平面垂直判定定理”教学为实例，深入探讨“5E”模式下“问题链"设计的具体策略与应用效果，旨在揭示该模式对学生数学思维发展的促进作用，为数学命题教学实践提供可借鉴的范例与参考建议

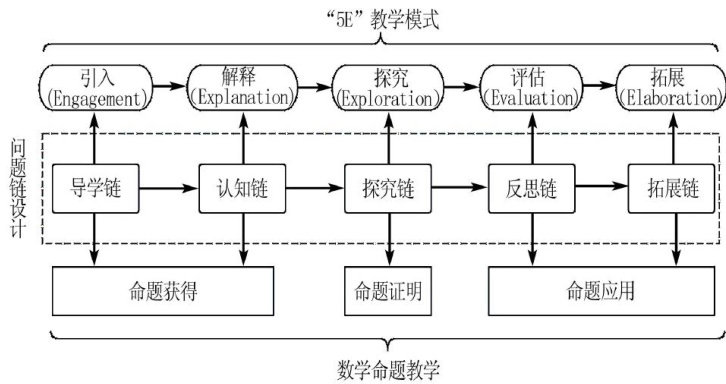
1 “5E”模式下数学命题教学中的“问题链”设计

1. 1 课堂模式构建

根据课堂教学环节设计，“问题链”教学法中的问题链分为导学链、认知链、探究链、反思链和拓展链.根据CPFS结构，命题学习的过程可分为三个阶段，即命题获得、证明、应用[3].各环节之间相互联系且层层递进，我们将“5E”教学模式中的五个阶段与之对应，得到图1.

1. 2 课堂实施策略

在数学命题的获得、证明和应用过程中，教师合理设置问题、安排课堂活动，有利于培养学生的逻辑推理能力，提升思维的灵活性.具体而言，教师可以通过以下几个步骤实施策略：在命题获得阶段，教师可利用导学链，结合情境导人提出初始问题，引发学生的兴趣和思考；在认知链环节，通过一系列由浅入深的问题，引导学生逐步深入理解命题的基本概念;进人探究链后，鼓励学生自主或小组合作，针对核心问题进行深入探究，教师适时提供必要的指导和资源；在反思链环节，组织学生进行成果展示和交流，通过互相质疑和解答深化对命题的理解；在拓展链环节，教师设计一些具有挑战性的问题，鼓励学生进行拓展思考和应用，进一步巩固和提升逻辑推理能力。（剩余4611字）