解决落点有约束的平抛运动

打开文本图片集

1落点在平面上

落点在平面上的平抛运动问题可细分为竖直平面、水平面和斜面三类，其中考查频率最高的是落点在斜面上的情况.

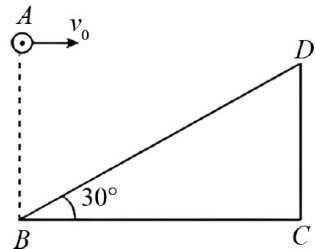
例1如图1所示，水平地面放有倾角为 30∘ 的斜面，小球从斜面底端 B 的正上方A点水平抛出，初速度为 v0=10m/s ，恰好垂直落在斜面上.

（1）求小球从抛出到落在斜面上所用的时间；

（2）求点 A 和点 B 间的距离.

图1

图2

解析根据小球垂直落在斜面上这一信息，可在落点处对小球的速度进行分解，由分速度关系求出小球落在斜面时竖直方向的分速度.因为小球做平抛运动，所以由 vy=gt 即可求出小球从抛出到落在斜面上所用的时间；再根据公式 x=v0t，h= gt²，可求出点A和点B间的距离大小.

（1）小球做平抛运动，当小球垂直落到斜面时，对其速度进行分解，如图2所示，可得 tan30=。（剩余1285字）