探究牛顿第二定律在连接体问题中的应用

打开文本图片集

连接体是指两个或两个以上相互连接、存在相互作用力的物体系统.它们通常通过轻绳、轻杆、弹簧等连接，具有相同的运动状态（如加速度大小相同).解决此类问题的关键在于正确处理物体间的内力与外力，合理选择研究对象.

1轻绳连接下的滑轮系统

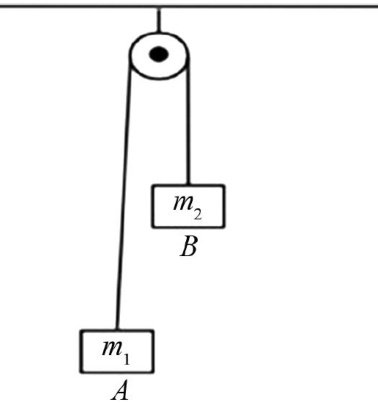
例1如图1所示，质量分别为 m1 和 m2 的物体 A 和 B 通过轻绳跨过光滑定滑轮连接，其中 m1>m2 .不计绳与滑轮间的摩擦，求系统的加速度大小及绳中张力.

图1

解析由于滑轮光滑且轻绳不可伸长，两物体加速度大小 a 相等，方向分别沿轻绳方向向上和向下.选择物体 A 和 B 为研究对象，分别进行受力

分析.

对物体 A ：质量为 m1 ，受重力 m1g 向下，绳拉力 T 向上，其合力产生向下加速度 a ·

由牛顿第二定律 ∇:m1g-T=m1a①

对物体 B ：质量为 m2 ，受重力 m2g 向下,绳拉力 T 向上，其合力产生向上加速度 αa .注意到加速度方向与受力方向需协调，通常以加速度方向为正方向更为简便.若设定加速度方向为正,则： T-m2g=m2a②.

将 ① 两式联立解得系统加速度：

将 a 代人 ② 式可得绳中张力：

点评本题亦可采用整体法求解加速度：将两

物体及轻绳视为一个系统，系统所受合外力为两物

体重力之差 (m1-m2)g （方向与加速度 Δa 方向一

致)，系统总质量为 (m1+m2 ).由牛顿第二定律直

接得： (m1-m2)g=(m1+m2)a ,解得 中但求内力（张力 T ）仍需使用隔离法.

2水平面内的连接体系统

例2如图2所示，在光滑水平面上，质量分别为 m1 和 m2 的物体 A 和 B 用轻绳连接，在物体 B 上施加一水平恒力 F ，使两物体一起向右加速运动.求系统的加速度及绳中张力.

图2

解析由于水平面光滑，系统仅受外力 F 作用，在水平方向上，系统所受合外力为 F .两物体通过轻绳连接，具有相同的加速度 αa

采用整体法：将 A,B 视为一个系统，系统所受合外力为 F ，总质量为 (m1+m2) .由牛顿第二定律 F=(m1+m2)α ，解得加速度：

为求绳中张力 T ，需使用隔离法.通常隔离受力较简单的物体，例如隔离物体 A ：它仅受绳拉力T （向右）作用产生加速度 a .由牛顿第二定律： T=

若隔离物体 B ，它受外力 F （向右）和绳拉力T′ （向左， T′ 与 T 为作用力与反作用力，大小相等)作用，合力产生加速度 α:F-T=m2α 代人 a= ,同样可得T=F-m2a=(m1+m2）。（剩余3496字）