高中物理热学题解题技巧与实例分析

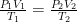
打开文本图片集

热学是高中物理体系中连接宏观现象和微观本质的分支，热学包括定量描述气体状态变化，还涉及能量转化与守恒的规律.热学具有“宏观现象复杂、微观机理抽象”的特点，学生解题时常陷入“公式记忆清晰却不知何时应用”“状态参量混淆导致计算失误”等困境.热学问题的解决不是仅依赖公式堆砌，学生需要建立“过程分析一规律匹配—量化计算”的逻辑.本文借助典型例题进行解析，来梳理热学解题的核心技巧，帮助学生突破“知其然，不知其所以然”的瓶颈，实现从知识记忆到思维应用的跨越.

1热学解题的核心思路与原则

热学问题的解决需以基本概念和规律为基础，结合分析方法.热学解题的思路可概括为“三步法”：

第一，学生明确研究对象与过程，热学问题涉及气体、液体、固体的状态变化，学生解题时需确定研究对象（如一定质量的理想气体)，分析过程特征（如等温、等压、等容或绝热过程).

第二，学生选取适用规律与公式，学生根据过程特征选择物理规律，如： （适用于任意理想气体状态变化)； ΔU=Q+W （能量守恒在热学中的应用)；=T P2 （等容过程专用）；=T 等压过程专用).

第三，学生要统一单位、规范计算，热学公式中物理量的单位需统一，如温度需用热力学温度开尔文(K)，压强单位可统一为帕斯卡 (Pa) ，体积单位为立方米 (m3) .学生计算时需注意符号规则（如热力学第一定律中，外界对气体做功W为正，气体对外做功为负；气体吸热 Q 为正，放热为负）.

2典型题型与解题技巧

2.1 理想气体状态变化问题

热力学方程是解决热学问题的重要工具，它描述了物质状态的变化和能量的转换.理想气体状态变化问题的关键是分析气体状态参量 (p,V,T) 的变化关系，明确过程类型后选择对应的规律求解.

例1一定质量的理想气体，初始状态为 P1= 1. 0×105Pa,V1=2. 0L,T1=300K 若经历等压膨胀过程后，体积变为 V1=4.0L ，求末态温度 T2 及气体对外做功 W .（已知大气压强恒为 1.0×105Pa)

图1

详解确定过程与规律：题目明确为"等压膨 胀",故适用盖－吕萨克定律 ，且做功公式 （204号 为 W=ρV （气体对外做功， W 为负).

代入数据计算温度：

计算做功大小：

体积变化 ΔV=V2-V1=4.0L-2.0L=2.0L= 2.0×10-3m3 ，

W=-ϕΔV=-1.0×105Pa×2.0×10-3m3= -200J.

因此，末态温度为 600K ，气体对外做功200J.

2.2热力学第一定律应用问题

热力学第一定律又称为能量守恒定律，是自然界中最基本的物理定律之一，在热学问题中同样适用.在热学问题中，这通常意味着热量从高温物体传递到低温物体，直到两者达到热平衡.掌握能量守恒定律，可以帮助我们分析和解决涉及热量传递的问题.热力学第一定律涉及内能变化(△U)、热量(Q)和功（W）的关系，解题关键是明确各物理量的符号及理想气体内能的决定因素（仅与温度有关）.

例2一定质量的理想气体在绝热容器中被压 缩，外界对气体做功500J.已知气体初始温度为 27∘C ，求气体末态温度（已知气体定容比热容 cV= 750J/kg⋅K ，质量 m=0,1kg, 。（剩余2786字）