高阶思维能力视角下初中数学教学策略

——以“二次函数”为例

打开文本图片集

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2025）20 -0051 -03

新课程改革背景下，学科教学的重点不仅是传授基础知识，更要在知识传授过程中培养学生的思维和能力，而学生的思维呈现出进阶发展的特点，以课时内容为依托的教学活动很难满足学生的学习需求.故而，立足单元教学，引入结构化教学理念，能够帮助学生构建知识框架，提高学生分析问题和解决问题的能力，促使其提升高阶思维能力，

1高阶思维能力视角下初中数学优化策略

二次函数是初中数学知识体系的重要组成部分，蕴含丰富的核心素养培养资源.笔者以“二次函数”教学为例，分析初中数学单元教学路径，落实思维进阶发展目标，提升学生的数学核心素养.

1.1 明确单元整体教学框架

思维指向个体的认知发展情况，思维进阶的过程是个体认知水平从低到高的发展过程.回归到初中数学教学，高阶思维能力视角下的教学策略应该参照学生的认知发展规律，将思维进阶的理论成果转化为数学教学的实践路径，即教师要从宏观角度规划目标、任务、评价等要素，促使学生跨越思维的“阶”，发展问题解决能力[1].首先，教师将“二次函数"单元内容划分成四个进阶维度，每个维度指向一个子单元.在此基础上，教师为子单元设计教学目标和情境任务，学生通过完成系列任务，实现单元学习目标，发展进阶思维，从而提升高阶思维能力.

1.2 定位单元整体教学目标

1. 2. 1 二次函数进阶维度

进阶维度又称为进阶变量，主要指向与核心概念相关的内容，能够充分反映学生对核心概念的理解程度.学生的思维发展过程不是一蹴而就的，是通过一个个子概念的学习而逐步建立起来的.在初中数学学习过程中，学生通过搜集资料、专项训练、知识探究等方法攻克教学难点和重点问题，掌握子概念的相关内容，再将子概念结合起来，形成完整的核心概念，最终实现思维进阶发展.由此可以推断，学生学习二次函数的过程也需要经过多维度的进阶发展，后一个维度的学习在前一个维度的基础上进行.“二次函数”单元知识的学习指向四个进阶维度，即概念认识、性质理解、实际应用、关联拓展.其中，概念认识的教学重点是建立基本的感知系统，对单元内的知识进行初步扫描；性质理解的教学重点是分析和应用，与二次函数图象性质相对应;实际应用的教学重点是实践操作，学生利用所学知识解决真实的问题;关联拓展的教学重点是创新、内化和迁移，学生要理解方程和不等式的用法2.起点是学生当前所处的位置，即思维发展的现状，终点是学生经过单元学习后要达到的结果，起点和终点之间的层级便是进阶维度.高阶思维能力是学生在感知、分析的基础上开展实践和应用的能力，是发生在较高认知水平层次上的心智活动或认知能力，它在教学目标分类中表现为分析、综合、评价和创造

1.2.2 二次函数进阶目标

基于对进阶维度的分析，教师可以从以下几个方面定位二次函数的教学目标.概念认识层面：学生要掌握函数、反比例函数、二次函数的概念，了解反比例函数与二次函数之间的关系，发展模型思想以及符号意识.性质理解层面：学生要学会分析函数图象的绘制流程，并能够清晰明了地画出图象，理解图象的性质，提升数形结合思想.实际应用层面：学生能够获取问题解决的思路以及关键信息，并在情境中解决问题；学会用数学的眼光观察生活，建立数学学习与生活之间的联系[3].关联拓展层面：学生能够将函数与方程联系起来，借助函数图象解决方程问题；提升迁移和应用能力，

1.3 设计单元整体教学任务

任务是初中数学教学策略的实践载体，在高阶思维能力视角下，教师不仅要在宏观层面规划单元教学方向，明确每个子单元的核心任务，还要在微观层面组织丰富的教学活动，确保核心任务落到实处，使学生通过子单元的学习逐渐建构单元大概念.

1.3.1 宏观规划单元任务

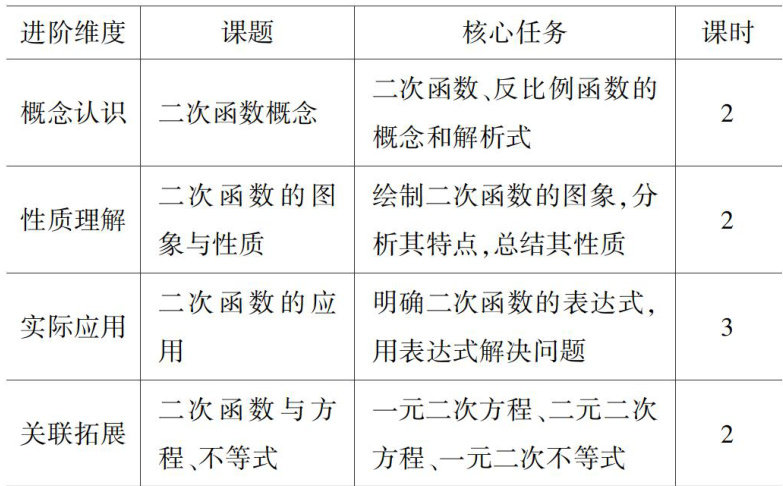
在初中数学教学中，单元任务的规划离不开单元内容的梳理，教师分析指向二次函数的碎片化知识，并将知识整合到一起，划分为不同的模块，以此规划“二次函数”单元任务，如表1所示.

根据表1，学生的思维逻辑按照“认识一理解—应用一拓展”的思路发展，在课时教学设计时，教师也应该遵循思维发展逻辑，循序渐进地提高学生的高阶思维能力。（剩余2215字）