高中数学创新题型的解题思路分析

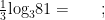
打开文本图片集

在当前教育改革不断推进的背景下，高中数学考试中注重考查学生的创新能力.创新题型是高中数学试卷中的特色部分，打破了传统题型的固定模式，具有独特的命题风格.该类题目将多个知识点进行有机融合，创设新颖的问题情境，要求学生在大量的信息中准确提取关键内容，灵活运用所学知识，进行创新性思考，以解决从未接触过的问题.创新题型的出现是对学生数学知识掌握程度的检验，综合考查学生的逻辑推理能力与创新意识.学生掌握创新题型的解题思路，有助于在考试中取得优异成绩，培养适应社会发展所需的创新思维.因此，对高中数学创新题型的解题思路进行深入分析具有重要的现实意义.

高中数学新定义型问题是在题目里给出高中数学未涉及的新概念、新运算以及新符号，要求学生先读懂题意，结合已掌握的知识去理解新内容，依据新定义开展运算、推理，以及知识迁移的一类题型，

新定义型题目主要考查学生对“新定义”的理解与认识程度，以及灵活运用知识的能力.在解题过程中，学生将“新定义”知识和已学知识建立联系，借助已有的知识经验解决问题.运用的数学思想如下：

（1）转化思想：将未知的问题转化为已学过的问题类型.当遇到新定义的函数问题时，可尝试利用变形、代换等方式，把题目转化为一次函数、二次函数等熟悉的函数类型，利用已掌握的函数性质与解题方法解决.

（2）迁移运用思想：在解读全新的概念的过程中，要能够灵活地进行知识迁移.在学习过程中，学生会积累很多不同类型的数学模型与解题策略.当遇到新定义问题时，要善于观察新定义与已学知识之间的相似性和联系，将已有的解题思路和方法迁移到新问题中.

在新定义的几何图形问题中，如果某些性质与已学的三角形或四边形的性质有相似之处，即可以借鉴处理三角形、四边形问题的方法解决新问题，

例1若 an=b（a>0 ，且 α≠1，b>0），n 即以 a 为底 b 的对数，记为 logab （即 logab=n， .如 34= 81，那么4叫作以3为底81的对数，记为 log381 （即log381=4; 。（剩余1651字）