依托“导主部分”，解决函数单调性问题

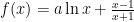
打开文本图片集

1 导主二次型

例1设函数 其中 a 为常数，讨论函数 f（x） 的单调性.

分析策略本题难度适中.首先确定函数的定义域为 （0，+∞） ，接着讨论函数的单调性，将 f（x） 求导 ax²+（2a+2）x+a，此时不能因式分解.由于分母项恒为正，现只需考虑分子部分的正负即可.显然，可以0为分界点进行讨论：当 a⩾0 ，此时f′（x）>0 ；当 a<0 时，判别式 Δ=4（2a+1） ，易求得 ，继续进行分类讨论.其中，当  时， Δ>0 ，因此函数 g（x） 有两个零点，且其开口向下，需要设出 g（x） 的两根 Φx1，x2 ，继续讨论.

解题过程 根据对数函数的性质，首先可确定函数 f（x） 的定义域为 （0，+∞） ，对函数求导得，   再根据函数定义域及导函数分母大于0进行分类讨论。（剩余1615字）