让学生形成“|a|-数轴-距离”思维

——突破绝对值概念理解壁垒的教学设计改进与思考

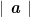
打开文本图片集

笔者第一次教授人教版七年级上册第一章第二节第4课“绝对值”时，对绝对值概念的理解不深刻，未引领学生突破绝对值概念的理解壁垒一—绝对值的几何意义，导致教学效果不佳.

经过进一步挖掘教材和课标，聚焦学生在绝对值概念上的理解壁垒一—绝对值的几何意义，精心转化书本知识，顺应学生思维发展规律，创设以“|α|一数轴一距离”为主线的探究活动，让学生真正理解绝对值的几何意义和代数意义，并能掌握求解绝对值相关问题的方法.现与大家分享“绝对值”教学设计的改进与思考.

1学生在绝对值概念学习上存在的主要问题

（1）对绝对值的几何意义理解较为肤浅，较难将绝对值与距离建立联系.（2）对绝对值的代数意义理解不够深入，特别是绝对值的非负性.（3）对绝对值知识的运用不熟练，尤其是对于含字母形式的绝对值问题，无法综合利用绝对值的知识以及相应的数学思想去解决.

2教学设计改进思路

2.1设置导入绝对值的问题情境

“绝对值"是七年级上册第一章的内容，学生正处于由具体运算阶段向形式运算阶段过渡的时期，且大多数学生更偏向于具体运算，思维形式无法摆脱思维内容，不具备成熟的抽象思维，形成心理疑难，具体的问题情境更有利于他们学习与整合绝对值的概念.

2.1.1注重新旧知识的衔接

问题情境1：

① 把下列各数及它们的相反数在数轴上表示出来： L4，-3.5，2.5，0，-1.5，（ ② 分别说出 ① 中的数在数轴上到原点的距离是多少？ ③ 数轴上4与—1.5的距离是多少？ ④ 数轴上2.5与它的相反数的距离是多少？

引导学生逐步解答以上问题，为引入绝对值概念奠定基础，让学生从已有知识（数轴、距离、相反数等概念）自然过渡到新知，实现新旧概念的衔接，2.1.2引入学生熟知的生活情境

问题情境2：

周五17时，7（4）班的2位老师驾驶汽车从黄陵中学出发，戴老师向东行驶 3km 回到家中，廖老师向西行驶 4km 回到家中，假设廖老师和戴老师的汽车行驶1km 消耗汽油量均为 0.08L ，思考并回答下列问题：① 若规定向东为正，则戴老师和廖老师行驶路线如何用正数和负数来表示？ ② 两辆汽车所消耗的汽油分别是多少升？ ③ 两辆小汽车所消耗的汽油与戴老师、廖老师的驾驶方向有没有关系？ ④ 两辆小汽车所消耗的汽油与什么有关？

问题情境2可以转化为图1，学生理解从学校出发回家，虽然戴老师行程路线是 +3 ，廖老师的行驶路线是一4，但两辆汽车消耗的汽油量分别是 0.24L 和0.32L ，都是正数，两辆汽车消耗的汽油量与行驶方向无关，仅与行驶距离有关.

引入学生熟知的生活情境，有利于理解在实际生活、生产中，有时并不需要考虑方向，仅需要知道距离即可[2]，为学习绝对值概念做铺垫.

2.2形成" |a| 一数轴一距离”为主线的探究活动

2.2.1引出绝对值的概念

在实际生活、生产中，很多情况下，不需要考虑数的正、负，比如我们坐网约车，到终点付费时，计费平台上的费用与网约车行驶的方向无关，与行驶的距离有关，距离只需用正数或0来表示，因此，人们引入了一个新的概念——绝对值[3].

引导学生感受绝对值概念的产生源于日常生活，帮助学生更好地感受绝对值的本质.

2.2.2理解绝对值的几何意义

教师引出绝对值这个全新的概念后，点燃了学生探究绝对值的欲望，基于学生在绝对值概念上的理解壁垒，先将绝对值与数轴取得联系，有助于学生理解绝对值的几何意义.

（1）建立“绝对值一数轴一距离"思维

探究活动1：

假设把小汽车行驶的路线想象成数轴，规定向东为正，将学校定为原点（数轴上的1个单位长度表示1km） 。（剩余3629字）