探究高中物理双导体棒在磁场中运动的综合问题

打开文本图片集

1引言

导体棒在磁场中的运动问题，由于其中涉及了电学和力学两大领域中的多个物理知识点，解题过程不仅复杂烦琐，且综合性极强.

2 等长双导体棒模型

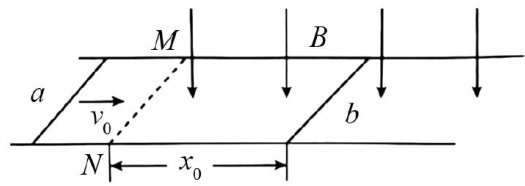
例1如图1所示，间隔为 L 且足够长的光滑平行金属导轨固定在同一水平面上，虚线MN右侧区域存在磁感应强度为 B 、方向竖直向下的匀强磁场.质量均为 Ψm 、长度均为 L 、电阻均为 R 的导体棒a，b ，垂直导轨放置且保持与导轨接触良好.开始时导体棒 b 静止于与MN相距 x⋅0 处，导体棒 a 以水平速度 v0 从MN处进入磁场.不计导轨电阻，忽略因电流变化产生的电磁辐射，且运动过程中导体棒 αa ，b 没有发生碰撞.试求：

图1

（1）导体棒 b 中产生的焦耳热；

（2）导体棒 b 中通过的电荷量；

（3）导体棒 Φa，b 间的最小距离.

解析（1）导体棒 a 进入磁场后，导体棒 aλ，b 及导轨组成的回路磁通量发生变化，产生感应电流.在安培力的作用下，导体棒 a 做减速运动、导体棒 b 做加速运动，直至二者的速度相等.在这一过程中，该系统的动量守恒，以 的方向为正方向，有 mv0= 2mu，再结合能量守恒定律，会有

Q. 导体棒 b 中产生的内能是 经过整理后可得 知

（2）以导体棒 b 为研究对象，根据动量定理，可得FΔt=mv ，而 F=BIL，q=IΔt ，联立上述三式可解得

（3）假设经过时间 Δt ，导体棒 aλ，b 的速度相等，此过程中安培力的平均值为 F ·

设导体棒 aλ，b 间的最小距离为 x ，以导体棒 b 为研究对象，根据动量定理，可得 FΔt=mv ，而 F= ΔΦ=BL（x-x） ，联立上式后可解得x=x。（剩余1548字）