高中数学“抛物线及其标准方程”相关习题的解题分析

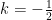
打开文本图片集

抛物线的定义、标准方程及几何性质是解答相关习题的基础.在具体解题过程中，需从抛物线的定义出发，结合题目所给条件，分析抛物线的标准方程.

例1已知抛物线 C:y2=4x ，定点 M(1,1) ，直线 l:y=kx+k+1

（1）当直线 ξl 经过抛物线的焦点 F 时，求点 M 关于直线 ξl 的对称点 N 的坐标，判断点 N 是否在抛物线 C 上.

(2）当 k(k≠0) 发生变化，且直线 ξl 与抛物线 C 存在公共点，设点 P(α,0) 关于直线 ξl 的对称点Q(x0,y0) ，求 x0 关于 k 的函数关系式 xΠ0=f(k) ：若 P 与 M 重合，求解 x0 的取值范围.

解析本题是一道综合题,结合了直线、抛物线与对称点的知识.给定直线与抛物线方程、一个定点 M ，在求对称点坐标时，充分利用中点坐标和斜率关系.在判断点是否在抛物线上时，准确地将点的坐标代入抛物线方程进行计算.

解(1)结合题意，由抛物线的焦点 F(1,0) 在直线 ξl 上，得 .所以 设点 N(m,n) ，则有

解得

所以 、

因为 ，所以点 N 不在抛物线 C 上.（2）将直线方程 代人抛

物线方程，可得 ky2-4y+4k+4=0 ，因为直线 ξl 与抛物线 C 相交，所以 Δ=16(-k2-k+1)≥0 且 k≠0 由对称得 解得

，且 k≠0; 。（剩余4481字）