解析几何中圆的公切线方程解题思路和技巧分析

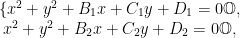
打开文本图片集

圆的公切线方程是对高中数学“圆的切线、切点弦”相关知识的拓展，该内容对学生的发散思维、逻辑思维以及应变思维能力都有一定要求.本文主要从解题思路和解题技巧两个角度对圆的公切线方程教学进行探讨.

1 圆的公切线方程简介

1. 1 圆的公切线方程

公切线是指同时与曲线 y=f(x),y=g(x) 相切的直线.圆的公切线是一种特殊的曲线公切线，通常以函数来表示，根据圆的性质可以将其分为外切公切线和内切公切线[1].当公切线位于两个圆的同侧时，则称该公切线为圆的外公切线，当公切线位于两个圆的不同侧，则称该公切线为圆的内公切线，如图1所示.

1. 2 圆的公切线方程解题思路

假设圆 O1:x2+y2+B1x+C1y+D1=0(B12 +C12-4D1>0⟩ ，圆 O2:x2+y2+B2x+C2y+ D2=0(B22+C22-4D2>0) ，并且两圆之间的关系为内切，则可以直接将两式联立后相减，得到经过两圆交点的直线即两圆公切线[2].

由 ①-② 可得： (B1-B2)x+(C1-C2)y+ (D1-D2)=0.

图1

两公式相减后代表的含义与两圆的关系存在关联：（1）当两圆为内切关系时，两圆的公切线仅有一条，此时两公式相减后得到仅有的公切线；（2）当两圆为外切或外离关系时，两公式相减后得到的公切线为两圆的内公切线，此时剩余公切线与内公切线平行或相交.

2 两圆内切的公切线解题技巧

两圆内切时，其公切线仅有1条，此时两圆的坐标关系如图2所示.

图2

计算两圆公切线时，可以直接将两圆的方程相减，得到两圆的唯一公切线，解题思路为：

例1计算圆 ⨀1:x2+y2-4x-16=0 ，与圆⨀2:x2+y2+2x-4=0 的公切线.

通过分析可以发现 ⨀2 的圆心 (0,-1) 在 ⨀1 的圆心内，并且两圆的半径相差等于圆心距，由此可以判断两圆的关系为内切，此时两圆公切线仅有1条，对于该内切两圆，可设公切线方程，利用圆心到切线距离等于半径的性质来解得公切线方程 2x+ y+6=0

3 两圆外切的公切线解题技巧

两圆外切可以分为两个半径相等的圆外切以及两个半径不等的圆外切，如图3所示.

图3

其中半径相等时的两圆外切公切线只需借助两圆半径以及外切线和内切线的平行关系则可以轻易求出，因此本文以例2分析两外切圆半径不等时的公切线计算方式.

例2过点 作圆 x2+y2=1 的两条切线，其切点分别为 A,B ，求

本题实质上可以通过作辅助外切圆的方式计算.首先假设存在与圆外切但半径不同的圆(x-n)2+(y-m)2=1 ，此时两圆相减后得到：2nx+2my-n2-m2=0 ,得到两圆的内切线,随后根据两圆内切线和外切线的几何关系，计算圆 x2+y2=1 与两圆的切线并得到切点，最终得出

两圆外离的公切线解题技巧

两圆外离可以分为两个半径相等的圆外切以及两半径不等的圆外切，如图4所示.

图4

其中半径相等时的两圆外里公切线只需借助两圆半径以及外切线和内切线的平行关系和相交关系即可以轻易求出，因此本文以例3分析两外离圆半径不等时的公切线计算方式.

例3计算圆 ⨀1:x2+y2=1 ，与圆 ⨀2 ·(x-6)2+y2=4 的所有公切线方程。（剩余1922字）