结合碰撞模型的多物体多过程运动问题探究

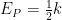
打开文本图片集

1弹簧模型 + 碰撞模型

例1如图1所示，在足够大粗糙水平面上有一质量 m=1kg 的长木板 C ，木板与水平面间的动摩擦因数为 μ1=0.1 、木板左端一小物块 A 以初速度v1=30m/s 滑上木板，此时木板上与 A 相距 27m 处有一小物块 B，A 与 B 的质量均是 m=1kg，A，B 与木板间的动摩擦因数均为 μ2=0.5 ，当 A，B，C 共速时，长木板右端恰好与自然伸长的水平轻弹簧的左端接触，假设 A 与 B 的碰撞时间极短， A，B 碰后粘在一起.已知弹簧弹性势能的表达式为 （Δx） 2 ，其中 k 为弹簧的劲度系数， Δx 为形变量，最大静摩擦力大小等于滑动摩擦力，重力加速度为g=10m/s2 ·

图1

（1）当 A 滑上木板 C 时，求 c 的加速度大小；（2）求 A，B，C 共速时的速度大小；（3）若木板压缩弹簧的过程中， A，B 与 c 恰不发生相对滑动，求弹簧的劲度系数和长木板 c 最终静止时其右端到初始时木板右端的距离 s

解析如图2所示，作出 A 滑上长木板到三者共速过程 A 和 B 的 v-t 图像，更易分析出每阶段不同物体的运动情况.

图2

（1）对A进行受力分析，有fcA=μmg=ma1，此时 B，C 加速度相同，对 B，C 这一整体进行受力分析，则有 fAC-3μ1mg=2ma2 ，可解得 a2=1m/s2 ：

（2）由于 A 与 B 相距 x=27m ，则有 Δx=xA-Δ xBC ，其中 at，可解得t0=1s 或 t0=9s（ （舍去）. A 与 B 相碰前瞬间 A 的速度为 v2=v1-a1t0，E B 的速度为 v′2=a2t0.A 与 B 碰撞瞬间， A 和 B 组成的系统动量守恒， mv2+mv′2= 2mv3 .碰撞后对 AB：2μ2mg=2ma3 ，对 C：2μ2mg- 3μ1mg=ma4 ，可解得 a⋅4=7m/s2 ， v4=a2t0=1m/s ABC共速时： ，可解得 t1= 1s ，v#=8m/s

（3）与弹簧作用过程中，对 ABC 整体： ;f∗+F∗∗= 3μ1mg+kΔx=3ma5.AB 与 c 相对滑动的临界加速度为 α5m=5m/s2 ，则 相对 C 恰不滑动，则弹簧压缩到 Δx′ 时， AB 和 C 的速度恰好减到零，根据功能关系可得知，－μ1·3mg△x-1。（剩余1613字）