电磁感应中线圈模型的分类与解析

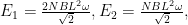
打开文本图片集

在历年高考中，命题者常常借助线圈模型，全面考查学生对电磁感应中电路、动力学、功能关系、动量与冲量等诸多知识的掌握程度.由此可见，线圈模型具有较强的综合性，若要顺利解答相关题目，势必要深入剖析该模型.

1静止线圈模型

在静止线圈模型中，线圈是不运动的，感应电流的产生都是通过磁感应强度的变化来实现的.在该类型的解题中，通常利用等效法，将线圈模拟成电路来分析，解题思路可分为以下四步： ① 电源分析，即找等效电源，求出感应电动势； ② 根据闭合电路欧姆定律分析电路； ③ 受力分析，求线圈所受安培力；④ 根据平衡条件列方程求解，

例1在图1中，有一个由硬质细导线制成的正方形线框放置在水平绝缘的粗糙水平面上，线框的边长为 L ，以其对角线MN所在直线为边界，左侧存在一个垂直平面向上的、磁感应强度大小为 B 按图乙所示规律随时间 ΨtΨt 变化的匀强磁场，右侧存在一个垂直平面向下的、磁感应强度恒定为 2B0 的匀强磁场.规定垂直平面向上为磁场的正方向，线框所用导线的电阻率为 ρ 、横截面积为 SΩ0 ，若 0～3To 时间内，线框始终静止，求：

图1

（1）在 T0 时刻，线框所受安培力；

（2）在 0～3T0 内，通过线框的电荷量.

解析 （1）T0 时刻，线框内的感应电动势 E= ，电流 左侧线框受到的安培力大小为 FE= ，方向向左；右侧线框受到的安培力大小为 ，方向向右.所以整个线框所受安培力的大小为 ，方向向右.

（2）在 0～3T0 内，通过线框的电荷量为 q=I ·

2 平动线圈模型

平动线圈模型是指在线框运动过程中其所在平面与磁感线的夹角不变化，该类型多涉及线圈穿越磁场区域的情况，解题思路与静止线圈模型类似，只是在分析受力过程时常需用到动能定理、动量定理、机械能守恒定律等知识点辅助解题.

例2如图2所示，在光滑绝缘的水平桌面（纸面）上固定一个间距为 L 的光滑长直金属导轨，导轨电阻可忽略，导轨左端连有定值电阻 R1=2R0 .在宽度为 2L 的区域有一方向垂直桌面向上的匀强磁场，磁感应强度为 B ，图中虚线代表磁场左右边界，两边界与导轨垂直.现将一边长为 L 、质量为 ψm 的正方形金属细框放在导轨上，与导轨接触的两条边与导轨平行.若已知金属框的每条边的电阻为 R0 ，让金属框以初速度 自左向右进入磁场，求金属框进入磁场的末速度，并判断其能否穿越出磁场.

图2

解析根据题意可将金属框右边等效为电源，左边视为与电阻 R1 并联，可知金属框进人磁场过程中电路的总电阻为R总=R。（剩余929字）