不规则图形面积的计算策略

打开文本图片集

在初中数学教学中，图形面积的计算是几何领域的重要内容，不仅关系到学生空间观念和图形理解能力的培养，更直接体现了其运算能力与综合思维水平的提升.与规则图形面积计算相比，不规则图形因形状复杂、边界不确定等特点，给学生的学习与解题带来了较大的挑战.基于此，探索科学、实用的不规则图形面积计算策略，成为提升学生几何思维和数学素养的重要突破口.本文中聚焦课堂教学与中考命题实际，系统梳理了三种常见且高效的计算策略：和差直接计算法、等积转换计算法、割补代换计算法.通过对策略内涵、适用情境及典型案例的深人分析，旨在为教师提供切实可行的教学指引，同时帮助学生建立灵活、多元的解题思维，提升其解决复杂几何问题的能力，真正实现知识的迁移与综合运用.

1策略一：和差直接计算法

1.1方法解读

所谓和差直接计算法，是指当要计算面积的图形是不规则的图形时，将不规则图形的面积转换成规则图形的面积，用转换成的规则图形的面积的和或差表示原来不规则图形的面积.

1.2图形解析

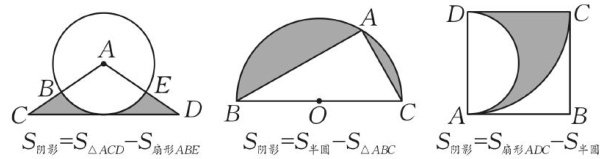
该策略适用于图形可以被识别并拆解为两个或多个规则图形面积的和与差，如扇形、三角形等.图1中，不规则图形通过扇形与三角形或半圆的面积相减构造得出，使原图形面积得以准确计算.

图1

1.3应用举例

例1如图2，在 RtΔABC 中， ∠CAB=90∘ ， ∠B=30∘ AC=8 ，以点 c 为圆心， CA 为半径画弧，交 BC 于点 E ；以点 B 为圆心， BA 为半径画弧，交BC于点 D ，则图中阴影部分的面积为 （结果保留 π 。（剩余1340字）