一道抛物线内三角切圆问题的求解探究

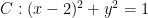
打开文本图片集

2021年高考全国甲卷第20题中以抛物线为载体，探讨了抛物线内三角切圆问题的一般证明，命题结构优美，改编题众多．在近期模拟题中，一道涉及周长与面积最值问题的求解或值得借鉴拓展。

1.题目呈现

（湖北省“宜荆荆恩”高三九月起点考试第11题）已知点 P 是曲线 ${ ＼boldsymbol { ＼itGamma } } _ { ： ＼boldsymbol { y } ^ { 2 } } = { ＼boldsymbol { x } }$ 上任意一点，过点 P 向圆 引两条切线，这两条切线与 的另一个交点分别为 ，则下列结论正确的有

A. B.直线 与圆 c 相切C．APAB的周长的最小值为 D. 的面积的最小值为

分析选项 A 只需要将点 P 置于坐标原点 o 即可推出矛盾；选项 B 即是借助同构思想刻画等量关系，求解圆心到直线的距离判断位置关系，即源于高考真题的直接应用；选项 C 与 D 本质相同，可先刻画 Δ P A B 面积表达转化为函数最值求解.故重点研究选项 B 与 D 的证明。（剩余1329字）