2024年全国甲卷理科第20题的多解与推广 浙江省诸暨中学 (311800)

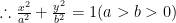
打开文本图片集

1.试题呈现

题目 （2024年高考全国甲卷理科第20题）已知椭圆 c 的右焦点为 F ，点 在椭圆 c 上，且 M F ⊥ x 轴.

（1）求椭圆 的方程；（ 2 ） P （ 4 ， 0 ） ，过 P 的直线与椭圆 c 交于 两

点， N 为 F P 的中点，直线 N B 与 交于 Q ，证明：AQ （20 轴.

2.多解探究

第（1）问易得 c 的方程为 （过程略）

下面重点探究第（2）问.第（2）问考查椭圆中的坐标问题，根据题目要证明的 A Q ⊥ y 轴，即转化为证明 两点的纵坐标相同.

证法1 当 A B 斜率为0时，显然 A Q ⊥ y 轴

当直线 A B 斜率不为0时，设过点 P （ 4 ， 0 ） 的直线为 x = m y + 4 ，与椭圆 c 的方程联立，消去 x 得（20 设 ， ，则

由 N 为线段 F P 的中点知， ，即 二2my2+3，直线BN：y 令 x = 1 2my+3要证AQ⊥y 轴 （2最后一式显然成立.故问题得证.

点评由于将直线设为 x = m y + 4 ，根与系数关系的式子更简洁，再结合分析法，进一步优化了证明过程，减少了计算量。（剩余1757字）