以直觉锁定特征 借目标优化运算

——函数极值点偏移的思考

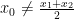
打开文本图片集

函数中极值点偏移问题在近七年的高考卷中出现了六次，且都处于试卷的压轴题位置.此类问题主要考查导数及其综合应用，涉及函数与方程、转化与化归以及数形结合等思想方法.该类问题尽管在平时的教学中也时有涉及，但涵盖的思想方法过于偏技巧.在近年的高考以及各种模拟考中，极值点偏移问题是一个热点问题.这类试题设问新颖多变，难度较大，综合性较强，可以较好地考查学生的逻辑推理能力.数据处理能力等.对于这类问题，学生通常会望而却步，甚至不敢解答，他们认为这种题目涉及面广、计算量大，害怕做“无用功”极值点偏移问题通常是指关于原函数f（x） 的零点与其极值点构成的不等关系的论证问题，体现学生的数学建模素养和创新思维能力.

以极值点偏移的多类解法为重要考查对象，尤其是含参与不含参的讨论[]，让学生理解“消元与引参”是问题转化的方向，“经验与逻辑”是问题解决的基础，以直觉锁定特征，借目标优化运算，从而提升学生的逻辑推理能力，让学生的解题活动从自发领悟走向自觉分析.本文将通过对函数极值点偏移和拐点偏移问题进行有效探究，提供有效方法.

1极值点偏移的含义

向左偏移;若极值点靠近右侧的xz，即x。（剩余2633字）