一道含参恒成立问题的多解探究

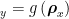
打开文本图片集

含参恒成立问题是近年高考数学中的必考点，此类问题往往具有一定的难度，而且对解题思维能力的要求较高.基于此，很有必要关注此类问题的多解探究，以便帮助我们迅速理解、掌握处理此类问题的常用解题思维方法，同时有利于较好地培养数学核心素养.

1好题采

已知函数 f（x）=x2+ax+b，g（x）=ex（cx+ （204号d ），若曲线 y=f（x） 和 都过点（0，2），且在点 P 处有相同的切线 y=4x+2

（1）求 ωa，ωb，ωc，dω| 的值；

（2）若 x⩾-2 时 f（x）⩽kg（x） ，求 k 的取值范围.

2多解探究

视角一：考虑作差构造函数法.一般地，遇到形如f（x）⩾g（x） 型的不等式恒成立问题时，常采用作差法，构造“左减右"的函数 h（x）=f（x）-g（x） 或“右减左”的函数 u（x）=g（x）-f（x） ，进而只需满足h （x）min⩾0 或 ，将比较法的思想融人函数中，转化为求解函数最值的问题.此方法适用范围较广，但是往往需要对参数进行分类讨论.

解法一：（1）由已知可得 f（0）=2，g（0）=2 f′（0）=4，g′（0）=4 ，而 f′（x）=2x+a，g′（x）= ex（cx+d+c） ，故 b=2，d=2，a=4，d+c=4 ，从而a=4，b=2，c=2，d=2.

（2）由（1）可得 f（x）=x2+4x+2，g（x）=2ex ·（x+1）

设函数 F（x）=kg（x）-f（x）=2kex（x+1）- x2-4x-2 ，则 2（x+2）（kex-1） .根据题意，有 F（0）⩾0 ，即 k⩾1. 于是，令 F′（x）=0 ，得

① 若 1⩽k2 ，则 -21⩽0. 当 x∈（-2，x1） 时， F′（x）<0 ；当 x∈（x1，+∞） 时， F′（x）>0. 所以函数 F（x） 在 （-2，x1） 上单调递减，在 （x1，+∞） 上单调递增.所以函数 F（x） 在 [-2，+∞ ）上的最小值为

F（x1） ，而 F（x1）=2x1+2-x12-4x1-2=-x1 ·（x1+2）⩾0 ，故当 x⩾-2 时， F（x）⩾0 ，即 f（x）⩽ kg（x） 恒成立.

② 若 k=e2 ，则 F′（x）=2e2（x+2）（ex-e-2） ，当x⩾-2 时， F′（x）⩾0 ，即函数 F（x） 在 [-2，+∞） 上单调递增，而最小值 F（-2）=0 ，故当 x⩾-2 时，F（x）⩾0 ，即 f（x）⩽kg（x） 恒成立.

③ 若 k>e2 ，易知 F′（x）⩾0 ，所以函数 F（x） 在[-2，+∞; 上单调递增，而 F（-2）=-2ke-2+2= -2e-z（k-ez）<0 ，故当 x⩾-2 时， f（x）⩽kg（x） 不恒成立.

综上所述，k的取值范围是 [1，e2]

视角二：考虑分离参数法.利用分离参数法处理含参不等式恒成立问题的主要思想是先实施分离参数变形，即将不等式变形成一边是参数 a ，另一边是变量表达式 F（x） 的不等式，再灵活运用以下常用结论求解目标问题.

常用结论：若函数 F（x） 存在最值，则不等式 Φa⩾Φ F（x） 恒成立 ⟺a⩾F （ρx）max ·a⩽F（ρx） 恒成立 ⇔a⩽ F（x）min·

解法二：（1）同解法一。（剩余1689字）