多维探究:基于深度学习的初中数学课堂教学

打开文本图片集

摘要：学生数学知识的获得需要在教师的引导下，在概念、定理、变式等多维课堂教学中创设探究环境，让学生主动去获取有效信息．在探究的过程中，学生再主动地创造、发现、获取更多其他有效知识，促使学生独立思考、理解数学，最终获取数学探究的能力．

关键词：深度学习;初中数学;课堂探究

当课堂还沉浸在“填鸭式”教育，即“教师讲讲讲，学生练练练”时，“双减”政策强势出台，使得这种教育的“最后一根稻草”终于承受不住了．在双减背景下，教师不得布置过重的作业，学生也没有机会在课后寻找培训机构重新补习．如何提高课堂教学质量迫在眉睫！

“深度学习”就是指在教师的引领下，学生能围绕具有挑战性的问题，全身心积极参与其中，并体验成功，最终获得发展的一个有意义的学习过程．在这个过程中，学生掌握科学的核心知识，把握学科的本质及思想方法，形成既具有独立性、批判性、创造性又有合作精神、基础扎实的优秀的学习者，成为未来社会实践的主人．

数学是一门锻炼个人思维能力，逻辑性、探究性很强的学科．作为数学教师，要在平时的教学中多引导学生进行课堂探究，让学生主动参与到发现问题、寻找答案的过程中，从而培养学生探究兴趣，最终解决问题．本文中将以不同的课型教学为例展开具体阐述．

１ 概念探究，培养学生的溯源能力

«义务教育数学课程标准»指出课程内容要符合学生的认知规律，它不仅包括数学的结果，也包括数学结果的形成过程和其中蕴含的数学思想方法．所以，即使是概念课也不仅要让学生知道概念的内容，更要让学生思考概念形成的过程，追本溯源，才能始得真意．

１．１ 概念教学课堂的探究设计

以浙教版七年级下册第一章的第２课时“同位角、内错角、同旁内角”为例，一般课堂中教师会直接提出同位角、内错角和同旁内角的概念，然后设计大量的巩固练习对概念进行辨析．这种教法使得学生只能被动地接受和记住同位角、内错角、同旁内角的概念．因此对概念进行探究很有必要，在探究的过程中让学生也当一回数学家，体验同位角、内错角、同旁内角的形成过程．具体探究过程可以如下．

首先回顾两条相交直线所产生的四个角（如图１，以下简称“两线四角”）的研究路径：角的两两组合———分类———命名———研究数量关系———得出结论．

回顾两线四角后，让学生在两线上增加一条线，学生会画出共点（如图２）和不共点（如图３）的两种情况，这时让学生自己去发现图２ 是在图１基础上的深化，而图３却不只有对顶角和邻补角，其他角可能也有研究价值．为了方便表达，我们将图３称为“三线八角”，那“三线八角”又该如何研究呢？ 此时，学生会很自然地类比“两线四角”的研究过程去研究“三线八角”．此时，放手让学生们自己去探究，学生会从以下方向去探究：

（１）将角进行两两组合，可以组成多少对角？

（２）利用角的位置关系，将角怎么分类？

（３）分类后的角该如何命名？

（４）角的数量关系该怎么研究呢？

在探究第（１）个问题时，教师可以引导学生探究不共顶点的一对角，那么学生比较容易得到：将不共顶点的八个角两两组合，可以产生１６对角．

第（２）个问题是利用角的位置关系，将角进行分类．此时需要对每一个角所在的位置进行统一规定，那么该如何规定呢？ 这就需要学生去探究，只要标准一致，怎么规定都没有关系．此刻的学生正像一位数学家那样在探索一个未知的领域，并且这个领域好像并没有那样的遥不可及．给学生以充足的时间去合作探究，

教师指导有困难的学习小组．在课堂上，教师能惊喜地发现学生的分类：

方法１：引用方位角，如∠１和∠５为东北角．

方法２：类似方位角，如∠１和∠５为右上角．

方法３：引用界限角，如∠１和∠５为同侧同位角．

……

分类后，名称就呼之欲出了，但是这个权利一定要先交给学生，让学生真正体验一把当数学家的成就感．当然很多学生对部分组合的角，如∠１和∠５的角，已经命名好，就叫东北角（右上角），也未尝不可．教师要做的事情是引导学生将所有的角进行命名，此时我们可借助巨人（教材）的力量，为了统一称呼，规定将形如∠１和∠５的角称同位角，形如∠３和∠５的角称内错角，形如∠４和∠５的角称同旁内角．教师也要带领学生去探索更广阔的知识领域，让学生模仿命名剩余的角．只要教师指明方向，学生的想象是无穷的，例如∠１和∠６会命名为异旁异部角，∠１和∠７为外错角，∠１和∠８为同旁外角……

１．２ 探究概念，追本溯源

我们花了大量的时间对１６对角的位置关系进行分类，首先是为了让学生追本溯源，理解数学研究的一般过程是类似的，即研究“三线八角”可以模仿“两线四角”的过程．同时学生对本节课之后的研究内容———角的数量关系，也有了研究方向．最后还解决了部分学生的疑惑：同位角、内错角、同旁内角这三类角命名的由来，以及除了这三类角，剩余的几对角又到底是什么角．通过对角的命名，学生获得了成功的喜悦，体验了学习数学的乐趣，激发了对数学探究的热情．

２ 定理探究，培养学生的质疑能力

数学定理是无需质疑的真命题．因此学生对于定理往往是全然接受，完全不会去挖掘定理中蕴含的秘密．殊不知，定理的产生本身就绝非一帆风顺，也是数学家像侦探一样经历多次尝试、冒险、质疑，验证，最后通过不断地打磨、精简得到的．

２．１ 定理教学的课堂探究设计

以浙教版八年级上册第２．８课时“直角三角形全等的判定”为例，在该课时中，用“HL”来证明两个直角三角形全等．但是“HL”和之前我们否定过的“SSA”有着类似的条件，这又是怎么一回事呢？ 这样的引导，势必会激发学生去质疑、探究．

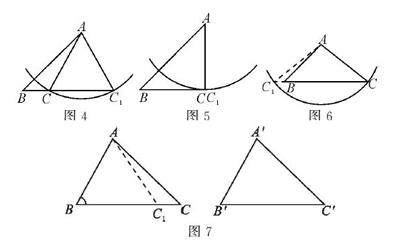
在设计该课时，教师可以先引导学生回顾利用“SSA”不能证明两个三角形全等时所采用的反例：如图４，AC＝AC１，AB＝AB，∠B＝∠B，但△ABC 不全等于△ABC１．接着借助几何画板，发现在构造图４时，是因为能构造出AC 和AC１ 两条相等的线段，如果拖动点C 向右移动，发现AC 和AC１ 两条线段重合（如图５）时，图形就唯一了，SSA 也就自然成立了，此时△ABC 恰好为直角三角形．接着学生必定会让老师继续将点C 向右移（如图６），发现AC１ 在△ABC 的外部，内部AC 唯一了，即SSA 也成立．采用几何画板演示不仅能让学生直观地发现图形的变化过程，更能发现问题所在，现只要将图４和图６进行对比，就能发现只要满足AC＞AB 即可．

于是问题就转化为：

如图７，在△ABC 和△A′B′C′中，AC ＝A′C′，AB＝A′B′，∠B ＝ ∠B′，AC ＞AB．求证：△ABC ≌△A′B′C′．

要证△ABC≌△A′B′C′，只要证BC ＝B′C′即可．假设BC≠B′C′，且BC＞B′C′．这样，在边BC 上就有一点C１，使BC１ ＝B′C′，所以△ABC１ ≌ △A′B′C′，故AC１＝A′C′．由题设AC ＝A′C′，可得AC１ ＝AC，故∠C＝∠AC１C．又因为在△ABC１ 中，∠AC１C ＞∠B，从而∠C＞∠B，由此AB ＞AC，这与题设中的AC ＞AB 矛盾，故BC≠B′C′不成立，因此BC＝B′C′成立[１]．

２．２ 探究定理，质疑辨惑

引导学生将上述结论的符号语言转化为文字语言，即“两边及其中大边的对角对应相等的两个三角形全等”这一定理，结合“HL”，发现“HL”的本质其实就是“两边及其中大边的对角对应相等的两个三角形全等”这一定理．

对于学生而言，对问题质疑正是激发他们去探索的动力，也是刺激他们去创造的源泉，教师一定要及时引导，不要错过真正培养学生数学能力的机会．经常给学生亲身研究和辨析定理背后秘密的机会，久而久之，势必会将冰冷的数学变成火热的思考。（剩余57字）