解答函数零点个数问题的三种途径

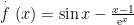
打开文本图片集

函数零点的个数问题侧重于考查函数零点的定义、零点存在性定理，以及函数的性质、图象.下面结合实例，谈一谈解答函数零点个数问题的三种途径，供读者参考.

一、利用零点存在性定理

在解答函数零点的个数问题时，我们经常要用到零点存在性定理.首先根据函数的解析式和已知条件确定函数的定义域，然后判断出函数在定义域内的单调性，再将区间的端点值代人函数的解析式，判断出两个函数值的乘积的符号.若其乘积小于0，则可以直接根据零点存在性定理，来判定函数在该区间上至少存在1个零点.

例1.请判断函数 在 π）上零点的个数.

解： 可得 ex⋅sinx-x+1=0 令藍 （则 所以 g′′(x)=2cosx⋅ex′(x) 在 上单调递减.（2 故存在 使樂 g′(x0)=0 ，则時 g(x) 在閣 上单调递增，在 (x0,π) 上单调递减：因为 所以 g(x) 雞在園 上有且仅有1个零点。（剩余3316字）