已知递推关系求通项an的几种技巧

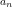
打开文本图片集

在高中阶段，等差数列与等比数列是数列模块的学习重点.在已知递推关系求解通项公式的过程中，常利用构造法将问题转化为等差数列或等比数列问题.在这一过程中，学生既要掌握数列的基础知识，又要分析题目所给条件，准确识别数列的类型.

1待定系数法

型数列 例1已知数列 满足 2，求 的通项公式.

因为 ，所以 1）.又 ，所以 是以9为首项、3为公比的等比数列，即 ，故

在探讨 （其中 A ， B 为常数，且 A ≠ 1 ， A B ≠ 0 ; 型数列的通项公式时，首先将原递推公式转换为 形式，其次运用待定系数法确定常数 M 的值，最后将原问题转化为等比数列问题求解.

型数列例2在数列 中，已知 （ 。（剩余1501字）