例谈高考数列不等式证明中通项放缩的策略

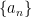
打开文本图片集

数列是高中数学的重要内容，也是高等数学研究极限的重要载体，是初等数学和高等数学的重要衔接点，更是各地高考中的热点和难点，而数列不等式的证明更是难点中的难点.此类问题所对应的数列一般不能直接求和，通常需要对通项或求和后的结果进行适当变形放缩后才能求和.放缩法的基本思想是通过放缩将原本不能求和的数列变成可以求和的数列.下面将结合具体例题分类归纳放缩的策略.

1放缩成等差数列求和

若数列 的通项公式是关于 n 的根式且根式化简后是 n 的1次式，可以考虑把它放缩成等差数列，如 n + 2 ：

一例1已知等差数列 的首项为1，前 n 项和为

（1）求数列 的通项公式；

（2）若 ，数列 的前 n 项和为 ，求证：

（求解过程略）.

（2）由（1）可知 所以 .由 ，可得

所以n（n+1） 又

所以n（n+1） ，即

先将数列 分别放缩成可求和的等差数列 和 ，再根据等差数列求和公式可证明.

2放缩成等比数列求和

若数列 是等比数列，数列 满足 ka，+b'则可以通过适当变形将b。（剩余2171字）