探究米勒张角问题

——教育数字化背景下的初中数学深度教学实践研究案例

打开文本图片集

为进一步激发学生的科学探索精神，培养其数学学科核心素养，推动初中数学深度教学课堂的构建，促进课堂教学模式的创新与变革，并辐射带动周边学校的发展，作者与6位教师共同组建了“名师课题研究团队”，在4所学校开展了系统的课例教学实践研究，取得了显著的教学成效与学习成果.现将其中关于米勒张角的探究案例整理成文，与广大数学教师及数学爱好者分享，以期为初中数学教学的深化与创新提供参考.

1背景问题

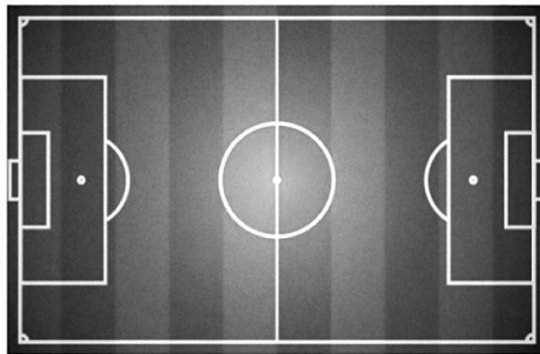
在一场足球比赛中，甲乙两队始终处于焦灼状态，比赛进入最后十分钟，双方依旧无法打破对方的球门.在需要球星挺身而出时，甲队一名具有远射能力的边锋球星，带球沿边路前进，在边线某处完成突破后突然起脚爆射，一记惊天远射进球打破了场上僵局，帮助球队取得了领先优势，请你用数学知识解释一下他选择起脚射门位置的科学性，

图1

为了从数学的角度搞清楚这个问题，探究小组设计了如下探究过程：第一步搜集有关球场的相关数据，第二步从这个具体问题中抽象出数学问题，第三步提出假设并验证，第四步逻辑推理，第五步从数学的角度找到依据，阐释球星的作用，第六步研究一般情况并总结相关结论，第七步应用探究成果解决问题，第八步查阅资料了解相关数学文化知识

2 探究过程

2.1 搜集数据

经过调查，本场比赛足球场地尺寸是世界杯决赛阶段足球场尺寸.如图1，球场长105米、宽68米，球门长7.32米、高2.44米，该球星打进这粒进球时的起脚位置是位于左边线距离对方球门底线34米处

图2

2.2 抽象问题

如图2，已知矩形 ABCD，AB=105 米， BC=68 米，边 AD 正中间有定长线段 EF=7.32 米，边 AB 上有一动点 P ，请问动点 P 从点 B 移动到点 A 的过程中， ∠FPE 是否存在最大值，如果存在请确定此时点P 的位置.

2.3 验证假设

根据数学经验，探究小组认为动点 P 从点 B 移动到点 A 的过程中， ∠FPE 是存在最大值的.为了验证假设，如图3，探究小组利用几何画板进行了验证，并应用“制表”功能记录了动点 P 从点 B 移动到点A的过程中 ∠FPE 部分过程性数据，通过观察发现动点 P 从点 B 移动到点 A 的过程中 ∠FPE 先变大后变小，所以可以确认假设是正确的.

图3

2.4 逻辑推理

如图4（鲁教版五四制九年级下册第五章第 4节），根据学习圆周角积累的经验.如图5，探究小组作出过点 P，E，F 的 ⨀o ，根据垂径定理可知圆心 o 始终在线段 EF 的垂直平分线上.当 OP⊥AB 时半径OP 最小，此时 ∠FPE 最大.作直径 PM ，连接 EM ，所以 ∠MEP=∠APM=90∘ ，所以 ∠EMP=∠APE ，因为 ∠EMP=∠AFP ，所以 ∠APE=∠AFP ，又因为∠A=∠A ，所以 ΔPAE～ΔFAP ，所以有  即AP2=AE⋅AF. 根据球场相关数据可以求出 AE =48.84 米 ∠AF=56.16 米，所以易求 AP≈33.8 米.

圆周角和圆心角的关系

在射门游戏中，球员射中球门的难易与他所处的位置对球门的张角（如图5-21中的∠ABC）有关。（剩余2317字）