数学教育的理性三境

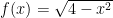
打开文本图片集

中图分类号：G632 文献标识码：A 文章编号：1673-8284（2025）06-0003-02

引用格式：数学教育的理性三境[J]．中国数学教育（高中版），2025（6）：3-4.

作为人类通过概念、判断、推理把握事物本质规律的一种能力，“理性”在数学教育中具有独特意蕴：《普通高中数学课程标准（2017年版2020年修订）》中12处提及这一概念，强调数学“在形成理性思维、科学精神过程中的不可替代作用”，要求培养学生“重论据、有条理、合乎逻辑的思维品质和理性精神”.反观教学实践，“理性”的落实常常陷入两重困境：或窄化为解题技巧的工具性，致其降格为机械操作模式；或虚化为道德说教的空泛化，割裂数学内在的逻辑根基．破局需要明辨数学教育理性的三重境界：奠基于方法论的理性思维境界，锤炼认知以把握数学本质；导向于价值论的理性精神境界，锚定信念而恪守逻辑必然；落脚于实践论的理性品质境界，规范行为并推动知行转化．这三重境界动态交融、协同发展，共同筑牢数学教育的理性根基，为学生数学核心素养的培养和完整人格的塑造奠定基础.

一、理性思维之境：学科素养的练就

理性思维是指通过抽象概括、逻辑推理、甄别验证、批判质疑等认知活动把握数学本质规律的思维能力，是数学学科育人的基础维度．思维境界的核心是培养学生从纷繁复杂的表象中提炼问题核心要素的能力，锤炼数学理性思维．数学教育若仅停留于公式演练，便会丢失育人的灵魂；唯有将思维训练贯穿于知识建构全程，才能培养真正的理性思考者.

以探究“对于函数 ，是否存在实数 k ，使 f（x）=k 有唯一解”为例，可以基于代数视角直接求解，将问题转化为“解方程 4-x2=k2 （k⩾0） ”（本质洞察），即 x2=4-k2 .要使该方程有唯一解，须有 4-k2=0 ，则 k=±2 （逻辑推演）.又因为 k⩾0 ，所以 k=2 （甄别验证）.也可以从几何视角抽象得出半圆模型（本质洞察），基于数形结合把问题转化为寻找水平直线 y=k 与该半圆的交点个数（逻辑推演），最终验证 k=2 时有唯一解（验证确认）.学生可能误用“求函数最值 f（0）=2 或定义域端点函数值 f（±2）=0 直接得解”的方法，但验证表明当 k=0 时对应两解，而 k=2 时有唯一解的产生是由特定几何位置决定的，并非普适方法（批判质疑）.据此引导学生感悟通性通法，学会具体问题具体分析，从而真正领悟该题理性思维的真谛（唯一解产生的特定条件），避免因直觉（或直观）上的疏漏导致逻辑谬误.此例通过代数推演与几何直观的互补协同，彰显理性思维的多元实现路径，深刻揭示了数学理性融通抽象与具象的独特价值.

二、理性精神之境：真理信仰的觉醒

理性精神是数学学科特性在人类意识中的价值投射，表现为对逻辑必然性的敬畏对真理的永恒追求，以及突破认知边界的开拓魄力，是数学教育的灵魂内核.精神境界旨在激发学生对真理的不懈追求和面对未知时直面挑战的探索热忱，厚植数学的理性精神，当学生真正明白“对数学规则的尊崇，源于其背后严密的逻辑必然；而敢于质疑，才是逼近真理的重要途径”时，理性思维便从解题的工具升华为支撑思想的信念，然而，部分教师对数学结论的讲授往往止步于“是什么”，却掩盖了“为何必须如此”的思辨空间，导致学生陷入算法崇拜而丧失对知识本源的敬重.

以三角函数诱导公式的教学为例.若教学仅以记忆“奇变偶不变，符号看象限”的口诀为终点，实质是将揭示规律性的数学真理降格为无需理解的操作指令，这种教法掩盖了公式背后的逻辑必然性，使学生沦为机械执行算法的工具．反之，可以引导学生追问核心问题：为什么角度增加 的奇数倍，正弦会变为余弦？通过坐标系中（单位圆上）角的终边的动态演示，使学生发现函数名变化的本质在于角度增加 奇数倍后，其终边与单位圆交点的纵、横坐标绝对值的角色互换.教师若回避这一几何本质，学生将错失理解公式内在逻辑的机会，从而难以建立“数学确定性源于严密推导”的认知．数学理性精神的价值在于使学生领悟：数学的可靠性源于逻辑必然性，而非记忆或权威；每一步推理都需要遵循这一必然性，而对“为什么”的持续追问，不仅是认知深化的推力，更是逼近数学真理的核心动力.

三、理性品质之境：知行合一的淬炼

理性品质是理性思维与理性精神在行为层面的具象化呈现，表现为严谨求实的学术习惯、自觉自律的细节把控和知行合一的价值践行，是理性人格落地的行为根基．品质境界重在引导学生在日常行为与学习实践中体现对严谨性的尊崇和对细节的自觉把控，培养数学的理性品质．当理性思维与理性精神在教学中交融渗透，其价值终将淬炼为自觉的行为习惯一这正是理性品质的内化过程．显然，这样的教学不再局限于教会学生解题，而是以理性品质的炼就为目标，引领学生养成严谨的思维习惯，历练批判性反思意识，确立求真的认知准则.

当前教学中，部分教师过度聚焦问题答案和解题速度，忽视学生的思维过程，且对推理严谨性与步骤规范性的关注不足，导致理性品质的培养流于表面．以立体几何的证明教学为例，若以“成功添加辅助线并得出结果”为终点，那么学生习得的可能只是一种技巧，倘若在证明线面垂直后追问：所用定理的每个条件是否在图形中可以直接观察或已严格证明？若将长方体替换为一般多面体，原来的证明方法是否仍能使用？则能引导学生系统性审视逻辑论证的严谨性．当教师将“推理过程的严密与规范”提升到与结论同等地位，学生方能真正理解理性品质的本质，即将对逻辑规则的恪守转化为“步步有据”的思维习惯与行为自觉.

四、理性三境交融：完整人格的塑造

理性三境的交融关系体现在它们之间的互动发展和相互依存上．思维是理性的根基，扎根于逻辑土壤；精神是理性的主干，支撑真理信仰；品质是理性的果实，体现知行价值．依循‘方法论奠基一价值论导向一实践论转化”的辩证路径，三者通过双向互馈、循环迭代，以实现动态融合．理性思维通过抽象和推理为理性精神奠基，使学生能透过数学符号把握宇宙规律的必然性；理性精神以真理追求驱动理性品质养成，让真理信仰外化为“每一步推导必有依据”的严谨和自律；理性品质又通过行为实践反哺理性思维，推动其不断走向深化．当学生规范细致、知行合一时，其思维的系统性和填密性也会推动理性信仰从对知识的单纯认可升华为对真理的追随和探究的热情.

数学教育中的理性思维、理性精神、理性品质三重境界通过“思维一精神一品质一思维”的闭环机制，构建起从认知能力到价值信仰再到行为自觉的系统性成长通道．这种动态融合，不仅是数学教育发展学生核心素养的重要路径，还是塑造学生未来完整人格的关键阶梯．诚如爱因斯坦所说：‘教育的目标不是学习知识，而是培养思维.”数学教育的终极目标亦非知识的机械记忆，而是理性素养的内化．当学生离校多年，具体的数学知识或许会被遗忘，但数学教育培养的理性思维、理性精神和理性品质终将融入其认知结构，沉淀为认识自我与理解世界的核心素养，为他们探索未知之境和应对未来之不确定性提供恒久的理性力量。（剩余0字）