妙用函数的奇偶性解答三类函数问题

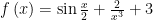
打开文本图片集

函数有四个重要性质，即单调性、奇偶性、周期性、对称性.奇偶性在解答函数问题中应用广泛，常用于求函数的值、判断函数零点的个数、解答函数的图象问题等.那么，如何运用函数的奇偶性解题呢？下面我们一起来作些探讨.

一、求函数的值

我们知道，在定义域内奇函数 f（x） 满足 f（x）+ f（-x）=0 ，偶函数满足 f（x）=f（-x）. 若已知函数是奇函数或偶函数，就可以根据 f（x） 的值来求 f（-x） 的值，反之亦然.

例1.已知函数 ，若 ⋅f（a）=5 ，则 f（-a）=.

解：令 则 f（x）=g（x）+3. 因为 是奇函数，所以 g（a）+g（-a）=0. 又f（a）=g（a）+3，f（-a）=g（-a）+3 所以 f（a）+f（-a）= 所以 f（-a）=1

虽然给出的函数 ⋅f（x） 不具有奇偶性，但可以把它看成奇函数 g（x） 与3的和，便可根据奇函数 g（x） 的性质得出 g（a）+g（-a）=0， 进而求出 f（-a） 的值.

二、解答函数的图象问题

我们知道，偶函数在定义域内关于 y 轴对称，奇函数在定义域内关于原点对称.在解答函数的图象问题时，我们可以先根据奇偶函数的定义判断出函数的奇偶性，然后根据函数的奇偶性找到函数在对称区间上的点，画出函数在对称区间上的图象.

例2.函数 的图象大致为（

解：由题意知函数 f（x） 的定义域为R，且 f（-x）= 所以函数 f（x） 为奇函数，其图象关于原点对称，故可以排除 C，D 选项.又当 f（x）>0 时 sinx>0 所以 2，可以排除B选项.故选A.

先根据函数奇偶性的定义判定 为奇函数，则其图象关于原点对称；然后讨论当f Φ（x）>0 时sinx的符号，进而判断出 x 的取值范围，从而排除错误的选项，找到正

确的答案.

三、判断函数零点的个数

具有奇偶性的函数的图象具有对称性，因而这类函数的零点也具有对称性.在判断函数零点的个数时，我们可以先判断出函数的奇偶性；然后根据函数的奇偶性来寻找对称区间上的零点，进而判断出函数零点的个数，

例3.已知函数 f（x） 在 （-∞，0）⋃（0，+∞） 上是偶函数，当 x>0 时， 请判断函数 零点的个数，

解：令g（x）=4f（x）-1=0可得f（x）=4当 0 可知 f（x） 在 （0，1] 上单调递减，在（1，2]上单调递增.而f（2）=1 ，则当 0 有2个交点.

当 x>2 时 当 2 ；当 4 ；当 6 则当x>2 时，函数 f（x） 与 有3个交点。（剩余319字）