四阶半正变系数常微分系统固结梁边值问题正解的存在性

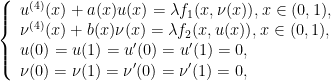
打开文本图片集

关键词：变系数；半正问题；拓扑度理论；正解中图分类号：0175.14 文献标识码：A 文章编号：1674-0033（2025）04-0014-05

Abstract：The boundary value problem of a four order semi-positive variable coefficient ordinary diferential system fora consolidated beam with two-end fixed-support boundary conditions，

∣u（4）（x）+a（x）u（x）=λf1（x，ν（x））， ，x∈（0，1）， ∣ν（4）（x）+b（x）ν（x）=λf2（x，u（x））， ∈（0，1）， u（0）=u（1）=u'（0）=u'（1）=0， ν（0）=v（1）=v'（0）=v'（1）=0，

it is studied by using the topological degree theory and Schauder's fixed-point theorem，where λ>0 isa parameter， a，b∈C [O，1]，and the nonlinear terms are continuous functions and satisfy certain conditions， the existence of positive solutions of the system is explored by constructing operators and proving relevant lemmas.When the nonlinear terms are continuous functions，satisfy the semi-positive assumption fi（x，0）

Key words： variable coefficients; semi-positive problem; topological degree theory; positive solution

四阶常微分方程边值问题是描述在弹性变形下梁状态的数学模型，也称弹性梁问题，理想的弹性变形条件对梁结构前期分析及后期延性调整起着至关重要作用。（剩余6514字）