求数列前 n 项和的几种思路解析

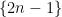
打开文本图片集

在解答数列问题时，我们经常会遇到求数列的前n 项和问题.解答这类问题，需掌握并灵活运用等差数列与等比数列的通项公式、前 n 项和公式.本文主要介绍求数列前 n 项和的三种思路，供大家参考.

一、分组求和

有时数列中的各项可以拆分、重组为几个简单的数列，如常数数列 1,1,1,⋯ ；等差数列 ；等比数列 ；等等.我们就可以采用分组求和法，将数列进行分组，分别进行求和，最后将各组的和相加减，就能求得数列的前 n 项和.

例1.设数列 的通项公式为 an=4n-1 ，且 为等差数列.若 b1=2 ， b2=6 ，求数列 的前 n 项和 Tn ：

解：设等差数列 的公差是 d ，由于 b1-a1=2-1=1,b2-a2=6-4=2 则 d=2-1=1 ，所以 bn-an=1+(n-1)×1=n ，即数列 的通项公式是 bn=n+4n-1 ，所以数列 的前 n 项和 T⋅n=1+40+2+41+⋯+ (n-1)+4n-2+n+4n-1=[1+2+⋯+(n-1)+n]+(40+41+⋯+(n-1)+n].

数列 的通项公式 bn=n+4n-1 可以拆分为 n ）4n-1 ，于是将数列 进行拆分，一组为等差数列：1,2,⋯,n-1,n ；一组为等比数列： 40,41,⋯,4n-2,4n-1, 分别运用等差数列与等比数列的前 n 项和公式来求和，即可解题.

二、裂项相消

若数列的通项公式可分裂为两项之差的形式，就可以考虑运用裂项相消法进行求和.将裂项后的各项重新排序、组合，使得前后项可以相互抵消，便能轻松求得数列的前 n 项和.运用这种方法求和，要仔细研究数列的通项公式，将其进行合理的裂项

例2.已知等差数列 的首项是3，公差是2，前n 项和是 Sn 求 的值。（剩余3998字）