轴向运动变长度梁的参数振动

打开文本图片集

中图分类号：0322;0323 文献标志码：A 文章编号：1000-4939（2025）04- 0792-09

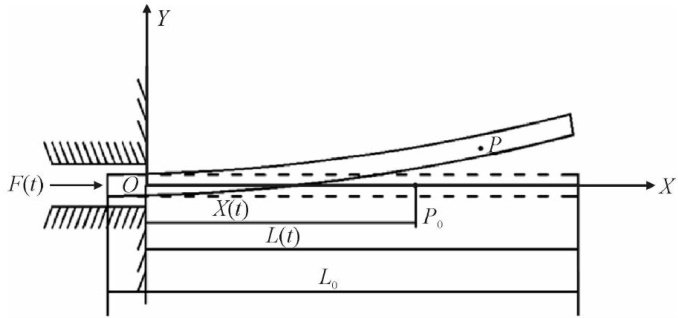
Abstract：The parametric stability of a cantilever-type beam of an axially moving variable length under the simple and harmonious excitationof length beam is studied.Based onthe Euler-Bernouli beam theory，the transverse vibration equation of a cantilever beam of an axially moving variable length is derived using the extended Hamilton's principle.For the dimensionless equation of the system，the system is discretized using Galerkin's method.And the ordinary differential equation of motion with time-varying coeficients is obtained.The parametric vibration characteristics of the cantilever beam with changing length in harmonic motion are analyzed by multiple scale method.It is found that the system has two types of instability ： primary resonance and combination resonance.The critical conditions are given for each instability domain. The influence of amplitude and frequency of length change on stability of the axially moving variablelength beam and the influence of the modal order on the type of system instability are discussed according to stability diagrams of system.The results show that the more modes involved in vibration，the more types of resonances the system has.The instability of the system is inhibited with the increase of the average length.The area of the unstable region increases as the average length of the system decreases.Finally，the correctness of the theoretical calculation of the multiple scale method isalso verified through numerical simulation.

Key words ：variable-length beam；axially moving；multiple scale method; parametric vibration； stability

轴向运动变长度结构在航空航天、机械、石油等工程领域[1-3]有着广泛应用，如空间站可伸展太阳能电池板、机器人伸缩手臂、可展开的空间附属物、油井钻柱、装载车辆的伸缩构件等。（剩余11158字）