复杂形状固支功能梯度板的弯曲问题分析

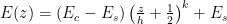
打开文本图片集

中图分类号：O341；TB301 文献标识码：A文章编号：1673-9868（2025）10-0181-14

Analysis for Bending Problems of Functionally Supported Gradient Plates with Complex Shapes

LI Shanqing1， SU Kexin1， YUAN Hong1 1，2

1. School of Mechanics and Construction Engineering，Jinan University，Guangzhou 510623，China;

2.Schoolof Architectural Engineering，Guangzhou Institute of Science andTechnology，Guangzhou ，China

Abstract： In engineering practice，analytical solutions for the bending problem of functionally graded plates are usually available only when the boundary conditions are simple. When constructing trial functions by means of numerical methods and the like to solve the problem，specific conditions need to be imposed， which is rather complicated. However，the R -function can solve this problem. This study incorporates the R -function theory with the variational method to deal with complex boundaries in the form of implicit functions，thereby facilitating the construction of trial functions that meet the boundary conditions. This paper elaborates on the variational principle and R -function theory，derives the variational equation for the bending problem of functionally graded plates，and validates the feasibility and accuracy of the method through numerical examples of rectangular， U-shaped， and L-shaped plates， presenting a novel approach for resolving the bending problems of functionally graded plates with complex boundaries.

Key words： complex shape; trial function; functionally graded plate; R -function theory； variational method

功能梯度材料广泛用于航空航天、生物医学工程、核工业、土木与机械工程等领域。（剩余13390字）