多视角解立体几何题的有效方法

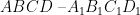
打开文本图片集

立体几何主要研究空间中的点、线、面及其相互关系。立体几何的解题通常涉及空间想象、图形构建、代数运算等多个方面，我们在解此类问题过程中常面临思维抽象、空间想象力不足等挑战。因此，在复杂的空间问题中掌握多角度的解题方法，对于提升我们的解题能力起着至关重要的作用。

一、例题

【例题】在长方体 中，已知 A B = 6 ， C B = 2 ， ，点 P 为底面ABCD内一点，若 和底面 所成角与二面角 的大小相等，点 P 在底面 的投影为点 Q ，则三棱锥 体积的最小值为

B.2 （20 D.32解：由题意， P Q ⊥ 平面 ， c ：： 和底面 所成角为 ， D过 Q 作 ，垂足为 M ，连接 P M ， MV由于 P Q ⊥ 平面 ， 平面 ， B1 C1： ， P Q ∩ M Q = M ， P Q ， M Q ？ 平面 平面PMQ， P M ？ 平面 P M Q ，：： 平面 P M ，则 为二面角 的平面角，即 。（剩余1607字）