基于李雅普诺夫指数的直齿轮非线性特性研究

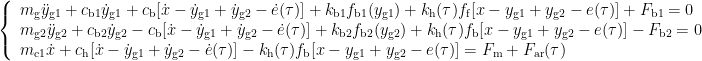
打开文本图片集

中图分类号：TH132 文献标志码：A 文章编号：1006-0316（2025）08-0007-07

doi：0.3969/j.issn.006-036.2025.08.002

Study on Nonlinear Characteristics of Spur Gears Based on Lyapunov Exponent

WEN Xue，2，LIU Yueming，ZHU Meiyu，²，DENG Chaofeng （.College of Mechanical and Energy Engineering，Shaoyang University，Shaoyang 422ooo，China;

2.Key Laboratory of Intellgent Manufacturing for Eficient Power Systems，Shaoyang 4220o0， China ）

Abstract ：In order to explore the influence of nonlinear factors on the motion of the single-stage gear transmission system，the influence of nonlinear factors such as backlash and excitation frequency on the vibrationofthesystemiscomprehensivelyinvestigated，andbytaking intoaccountthe longitudinal vibration displacement of the gear system，the nonlinear dynamic model of longitudinal displacement and torsional displacement coupling is established through the concentrated mass method，and the relevant dynamic equations are derived.The ode45 function is adopted to numerically solve the equation of state of the gear system. Combined with the maximum Lyapunov exponential diagram of the system，the bifurcation and chaotic characteristics with the excitation frequency and tooth clearance are analyzed，and the following conclusions are obtained： when the excitation frequency varies within [2.2，3.1]， with the increase of the excitation frequency， the system changes from single-periodic motion to chaotic motion，and finally returns to single-period motion through inverse doubling，and the corresponding Lyapunov exponent shows a negative-positive-negative change pattern; when the backlash varies within [O.06，0.075]，with the increase of tooth clearance，the system changes from a single-period motion to a chaotic motion，evolves into a four-period motion through doubling bifurcation， and finally becomes anunstable chaotic motion with a short periodic window，and the corresponding Lyapunov exponent alternates between positiveand negative values，especially frequent in the unstable chaotic region.The analysis resultscanprovidea theoretical basis forthe selection of gear excitation frequencyand the design of backlash.

Keywords：nonlinear dynamics;backlash;excitation frequency;chaos;bifurcation

齿轮传动系统运用于各种领域，其负载运行过程呈现出复杂的动力学特征，吸引了大量学者研究[1-2]。（剩余5142字）