分数阶非自治时滞发展方程初值问题解的存在性

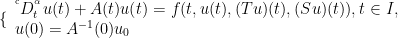
打开文本图片集

中图分类号：0175.15 文献标志码：A 文章编号：1671-5489（2025）05-1260-09

Existence of Solutions to Initial Value Problem of Fractional Non-autonomous Delay Evolution Equations

YANG Daixiong， ZHANG Xuping （College of Mathematics and Statistics，Northwest Normal University，Lanzhou 73007o，China）

Abstract： We used the Kuratowski measure of noncompactness and Sadovskii's fixed point theorem to study the initial value problem of fractional non-autonomous delay evolution equations in Banach spaces.We proved the existence of mild solutions to the problem under weaker noncompactness measures and growth conditions.

Keywords： fractional non-autonomous evolution equation； delay； condensing mapping; existence

0引言

分数阶自治发展方程是经典发展方程中整数阶导数被任意阶导数替代所得的发展方程．相比整数阶自治发展方程，分数阶自治发展方程能更好地刻画各种材料和过程的记忆性和遗传性．目前，具有时滞的分数阶自治发展方程在理论和应用方面受到广泛关注，并取得了一系列研究成果[-10]．自治发展方程中的线性主部算子 A 与时间 Ψt 无关，它对应于线性偏微分算子与时间 Ψt 无关的非线性偏微分方程．但许多非线性偏微分方程的线性主部算子通常与时间 t 相关，即线性偏微分算子不仅与空间变量有关也与时间变量有关．因此，一些学者开始研究分数阶非自治发展方程，其线性主部算子 A（t） 是与时间变量 Ψt 相关的无界算子．从而对分数阶非自治发展方程的研究可以使线性主部算子与时间变量 Ψt 有关的这类偏微分方程获得一般方法地解决.

EL-Borai等[1]首次研究了具有零初值的线性分数阶非自治发展方程解的预解式表示．朱波等[12]利用广义Banach不动点获得了一类带时滞和瞬时脉冲的分数阶非自治发展方程初值问题解的存在性和唯一性．Chen等[13]利用分数阶微积分理论和凸幂凝聚算子的不动点定理，获得了Banach 空间 E 中分数阶非自治发展方程Cauchy问题

温和解的存在性，其中 表示 α（0<α⩽1） 阶Caputo分数阶导数， I=[0，a] ， ∣a>0 是一个常数， 是闭线性算子，并且 D（A） 不依赖于时间 t ：

但目前许多关于分数阶非自治发展方程的研究均未考虑时滞的影响，而在实际系统中，时滞是不可避免的．基于此，本文在 -A（t） 生成的发展系统非紧的情形下，在Banach空间 E 中讨论一类分数阶非自治时滞发展方程初值问题

温和解的存在性，其中 表示 α（0<α⩽1） 阶Caputo分数阶导数， I=[0，a] ， A（t） ： D（A）⊂EE 是闭线性算子族，定义域 D（A） 不依赖于 Ψt ， 为Carathéodory函数，a，h>0 为两个常数， ϕ∈C（[-h，0]，E） 是系统本身选择的一个预先给定的函数，且

为积分算子，积分核 K∈C（Δ，R） ， ，H∈C（△。（剩余8309字）