基于改进鸟群优化算法的TDOA定位算法

打开文本图片集

中图分类号：TP391 文献标志码：A

TDOA Location Algorithm Based on Improved Bird Swarm Optimization Algorithm

YANG Man,REN Zhi-guo，XUE Pan-pan (School of Information Engineering，Lanzhou City University，Lanzhou 73oo7o，China)

Abstract:Aiming at the problems such as the complex solution of nonlinear equations encountered in the positioning of time difference of arrival, this paper proposes a TDOA positioning algorithm based on the improved bird swarm optimization algorithm. Firstly，the effects of different chaotic mappings were compared and analyzed. It was selected to use the Chebyshev chaotic mapping for the initialization of the bird flock to further improve the initial solution effect and enhance the population diversity. Secondly，set the acceleration coeficient in the foraging behavior of the bird flock as a nonlinear dynamic adjustment factor to balance the global search and local development capabilities of the population and avoid the algorithm falling into local optimum. Finally，based on different environmental parameters， the RMSE for positioning and solving by different intelligent algorithms was simulated and analyzed. The experimental results show that， compared with the traditional particle swarm， genetic algorithm and bird swarm optimization algorithm，the improved bird swarm optimization algorithm has a lower RMSE in solving the optimal solution of the TDOA nonlinear equation system.

Key words:time difference of arrival; bird swarm optimization； chaotic mapping；intelligent optimization algorithm

0 引言

20世纪80年代以来，智能交通系统的快速发展和蜂窝无线通信的广泛普及对无线定位技术提出新的要求和挑战，引起了国内外学者的高度关注并开展深入研究[1].基于到达时间差（TimeDifferenceofArrival，TDOA）的定位系统成本低、定位精度高等优势，已成为该领域的重要研究方向[2].

TDOA定位技术通过构建非线性双曲线方程组并对其进行求解，计算出移动台的位置坐标.目前常用算法在求解该方程组时存在性能受限问题，Chan氏算法[3性能受限于噪声特性，当噪声为非高斯随机变量或非零均值时，定位性能显著降低；Taylor级数展开法4作为递归算法，存在初始解依赖缺陷，当初始值设置不合理时不能计算出最终收敛结果;最小二乘法及其改进算法[5]在运算过程中涉及矩阵求逆问题，若测量值数量不当则会出现矩阵奇异或明显的门限效应.智能优化算法为解决上述问题提供了新思路，如粒子群算法（Particle Swarm Optimization，PSO)[6]、遗传算法(GeneticAlgorithm，GA)[7]、樽海鞘群算法[8]、哈里斯鹰优化算法[9]和蜉蝣算法[10]等通过并行搜索机制可以更快找到最优解.

鸟群优化算法（Bird Swarm Algorithm，BSA)[11是一种基于鸟群觅食行为的群智能优化算法，具有操作简单、参数少、运算速度快、鲁棒性好等优点，但也存在寻优后期缺乏种群多样性、寻优速度慢、易陷入局部最优等问题.文献［12]通过在BSA中加人自适应惯性权重实现动态调整搜索空间、改变收敛速度.文献[13]提出通过自适应感知系数、社会系数及学习因子优化飞行行为，不仅避免算法陷入局部最优，还保证个体寻优能力.

本文首先剖析了TDOA和BSA 的理论基础，提出一种改进鸟群优化算法（ImprovedBirdSwarmAlgorithm，IBSA);然后构建了基于IB-SA的TDOA非线性方程组求解算法；最后通过仿真实验，在二维空间中验证了所提算法在收敛速度、定位性能的优越性.

TDOA定位模型

1.1 定位原理

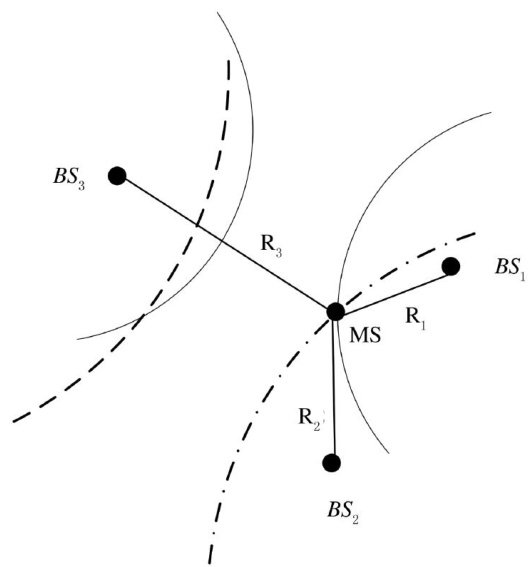
TDOA定位通过检测移动台信号到达两个基站的时间差实现移动台定位.由几何原理可知，平面内到两定点的距离差的绝对值为定长的点的轨迹叫做双曲线，因此TDOA定位又称为双曲线定位.

双曲线定位原理如图1所示，已知移动台MS到基站 BS1 和 BS2 的距离分别是 R1 和 R2 ，根据几何原理可知，移动台位于以 BS1 和 BS2 为焦点、以移动台MS到两基站的距离差 R2,1=R2- R1 为焦距的双曲线上.同理，如果得到移动台到基站 BS3 与基站 BS1 或 BS2 的距离差 R3,1 或R3,2 ，就可以构造出另外一条双曲线.这两条双曲线相交于两点，其中一个交点就是移动台MS的估计位置.通过求解 R2,1 和 R 3,1 或 R3,2 构成的方程组，则可以得到两个解，即这两条双曲线的交点，再根据小区半径等信息，就可以得到移动台MS的位置估计坐标.

图1双曲线定位原理

1.2 TDOA定位模型

二维平面定位系统中基站数目为 M(M) 3)，移动台MS的待定位坐标为 (x,y) ，第 i 个基站 BSi 的坐标为 (Xi,Yi) ，移动台MS到第 i 个基站 BSi 的实际距离为 Ri ，则

其中： τi 表示定位信号从移动台到达第 i 个基站

的到达时间真实值； c 为信号传播速度即光速.利用公式（1）将其转化为基站与移动台之间的距离：

Ri=cτi.

以 BS1 为服务基站，记MS到 BSi(i≠1) 和MS到 BS1 的真实距离差为 Ri,10 ，其测量值为Ri,1 ，则

Ri,1=c*τi,1=Ri,1∘+c*ni,1=

Ri-R1+c×ni,1,i=2,3,⋯,M,

其中： τi,1 为MS到 BSi 与 MS 到 BS1 之间的TDOA测量值； ni,1 为TDOA进行测量时系统正常存在的噪声.为了方便后续分析，将其理想化为服从独立同分布，且均值为0、方差为 σ2 的高斯白噪声，则

c*ni,1,i=1,2,⋯,M.

求解移动台MS的位置就是求解由 M-1 个公式（4）组成的方程组，即

ΔR=(R-R1)+c⋆n=

其中：

由上可知， ΔR 服从均值为 (Ri-R1) 、方差为σi 的高斯分布，又因各测量值之间是相互独立的，故方程组的最大似然函数可表示为

求解公式（6）相当于求解公式（7）的目标函数，即

(x,y)=

公式（7）的非线性特性导致解析法求解难以获取，故本文采用改进的鸟群优化算法求解目标函数的最优值，根据公式（7）可以推导出算法采用的适应度函数为

其中， X 为改进的鸟群优化算法中鸟群个体的位置.

2 鸟群优化算法

BSA中鸟类主要有3种行为：觅食、警惕和飞行.记 Ψt 时刻时第 i 只鸟的位置为 $\{ x _ { i , j } ^ { \ t } ( i \in [ 1 , 2 \$ ⋯,N],j∈[1,2,⋯,D]) .其中 N 为鸟群的个体数； D 为鸟群个体的维度.

传统觅食行为的位置更新公式为

xi,jt+1=xi,jt+(ϕbest-xi,jt)×

C×rand(0,1)+(gbest-xi,jt)×S×rand(0,1),

其中： ρbest 为第 i 只鸟目前最佳位置； gbest 为种群目前最佳位置； rand(0,1) 为服从（0，1）均匀分布的随机数；C和S是两个正常数.

警惕行为的位置更新公式为

xi,jt+1=xi,jt+A1×(meanj-xi,jt)×

rand(0,1)+A2×(ϕk,j-xi,jt)×rand(-1,1),

其中， k(k≠i) 为一个取值范围为 [1,N] 的随机正整数； 为两个取值范围为[0，2]的正常数； ∇pFiti 和 ϕFitk 分别为第 i 只鸟和第 k 只鸟的最佳适应度值； sumFit 为所有鸟群个体的适应度值之和； ε 是用来避免零除误差最小的常数；mean；为第 j 维所有个体的平均个体最优位置；当某一个体向鸟群的中心位置移动时，周围环境引起的影响由 A1 表示，特定干扰引起的影响由A2 表示.

FQ为一个正整数，用来表示鸟群飞行的单位间隔.此时，一些鸟类作为生产者寻找食物块，而另一些则作为乞食者试图从生产者找到的食物块中觅食.它们的位置更新公式分别为

xi,jt+1=xi,jt+(xk,jt-xi,jt)×FL×rand(0,1),

xi,jt+1=xi,jt+randn(0,1)×xi,jt,

其中： randn(0,1) 表示均值为0、标准差为1的高斯分布随机数； k(k≠i) 表示取值范围为 [1,N] 的随机正整数； FL∈[0,2] 表示搜索者会跟随生产者搜索食物.

3改进的鸟群优化算法

3.1 改进的初始种群

针对BSA算法在问题求解时因初始化质量低而导致的种群多样性不足问题，提出混沌映射初始化改进方法.混沌变量因其随机性、遍历性和规律性特点，能够生成均匀性的初始种群，有效保持种群的多样性.目前比较常用的混沌映射有Chebyshev映射、Logistic映射、Tent映射和Ber-noulli映射[14].4种混沌映射的序列图和散点图如图2和图3所示.

（a）Chebyshev映射

8 0 。（剩余11544字）