如何解答平行线中的折线问题

打开文本图片集

平行线是几何中最基本的概念之一.借助平行线的性质，可以推导出角之间的相等或互补关系，从而解答与角度相关的问题.然而，当两条平行线并非被一条直线所截，而是被一条折线所截时，便构成了“平行线中的折线问题”.这类情况下，平行线的性质定理无法被直接应用.那么，应如何解答此类问题？下文将分类进行探讨.

一、平行线中“外凸型”折线问题

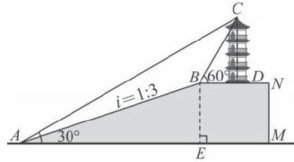
“外凸型"折线问题是指两条平行线之间被向外凸出的折线所截，并有一个或多个折点.解答这类“外凸型"折线问题的一般方法是过折点作已知平行线的平行线，通过形成所以 BE=10 （米），所以平台BN的高度是10米；

图6

图7

(2)如图7，延长 CD 交 AM 于点 F

因为 CD⊥BN ， BN//AM ，

所以 CD⊥AM ，

所以四边形BDFE是矩形，

所以 DF=BE=10 米， BD=EF ，

设 CD=x 米，则 CF=CD+DF=x+10(∗ ），

因为在 RtΔACF 中， ∠CAF=30∘ ，

所以

（米），

因为在 RtΔBCD 中， ∠CBD=60∘ ，

的多组平行线建立分散的角与角之间的联系，进而把线的关系转换成角的关系，然后利用“两直线平行，同旁内角互补”的性质解答.

例1如图1,已知 AB//CD ， ∠A=120∘ 5∠C=130∘ ，那么 ∠APC 的度数是( ）.

A.100∘ B.110∘ C.120∘ D.130∘ 解析：过 P 作直线 MN//AB ，如图2所示，： ⋅MN//AB ，

图1

图2

所以 _，所以 （米），由(1)有 AE=3BE=3×10=30 （米），因为 AF=AE+EF ，所以√3（x+10）=30+√ ，解得 ，所以 （米），即建筑物的高度(即 CD 的长)为 米.

总之，解直角三角形是连接数学理论知识与现实世界的"桥梁”，其应用贯穿于测量、工程、航海等诸多领域.掌握解直角三角形的方法，不仅有助于同学们巩固三角函数、勾股定理等基础知识，更能够培养他们从实际情境中抽象出数学问题、构建模型并求解的思维能力.

·.∠A+∠1=180∘ （两直线平行，同旁内角

互补)， ∵MN//AB,AB//CD ∴MN//CD ，·⋅∠C+∠2=180∘ （两直线平行，同旁内

角互补)，∴∠2=180∘-∠C=180∘-130∘=50∘ ∴∠APC=∠1+∠2=60∘+50∘=110∘ 故选：B项.

点评：本题考查了平行线的性质，解题的关键是作出平行线，根据平行线的性质找出图中角度之间的关系，由此得出结论：在平行线中有一个折点的“外凸型”折线问题中，中间角加两个边角等于360度，即 ∠A+∠P+∠C= 360∘ ：

例2细观察，找规律．下列图 ①①① 中的 MA1 与 NAn 平行

图3

（1）图 ① 中的 ∠A1+∠A2= 度，图 ② 中的 ∠A1+∠A2+∠A3= 度，图 ③ 中的 ∠A1+∠A2+∠A3+∠A4= 度，图 ④ 中的 ∠A1+∠A2+∠A3+∠A4+∠A5= 度，…，(2）第 n 个图中的 ∠A1+∠A2+∠A3+⋯+ (3）以图 3② 为例，写出证明过程

分析：(1)根据两直线平行，同旁内角互补，即可得到结论；(2)根据(1)中的规律，即可得到第 n 个图中的 ∠A1+∠A2+∠A3+⋯+∠An+1 的度数；(3)先过 A2 作 A2B//A1M ，根据 A2B// A1M//A3N ，可得 ∠A1+∠1=180∘ ， ∠A3+∠2= 180∘ ，进而得出 ∠A1+∠A1A2A3+∠A3=360∘

解：(1)根据平行线的性质，可得图 ① 中的 ∠A1+∠A2=180 度，根据平行线的性质，可得图 ② 中的 ∠A1+∠A2+∠A3=360 度，

根据平行线的性质，可得图 ③ 中的 ∠A1+

∠A2+∠A3+∠A4=540 度，根据平行线的性质，可得图 ④ 中的 ∠A1+

∠A2+∠A3+∠A4+∠A5=720 度，故答案为： 180,360,540,720 (2)根据平行线的性质，可得第 n 个图中

的 ∠A1+∠A2+∠A3+⋯+∠An+1=180∘n. 故答案为： 180∘n (3)如图 4② ，过 A2 作 A2B//A1M ： MA1 与 NA3 平行，∴A2B//A1M//A3N ·.∠A1+∠1=180∘ ∠A3+∠2=180∘ 又： ∠1+∠2=∠A1A2A3 ：： .∠A1+∠A1A2A3+∠A3=180∘+180∘=360∘. M AM 4 M A

M AB- As

N ① AN ② AN ③ A4N ④ A5 A4

点评：本题通过四个特殊的图形得到了一般性规律，运用了不完全归纳法，体现了由特殊到一般的数学思想.这是解答规律探索题时的常用方法.通过例2总结的一般规律可以得出结论：对于平行线中有多个折点的“外凸型”的折线问题，有一般性结论：折线内角的和 σ=σ （折点数 +1)×180∘ ：

二、平行线中“内凹型"折线问题

与平行线中的“外凸型"折线问题相对应，平行线中也有“内凹型"折线问题.“内凹型"折线问题是指两条平行线之间被向内凹进去的折线所截，并有一个或多个折点.解答“内凹型”折线问题，通用的方法仍是过折点作原平行线的平行线，形成多组平行线，然后利用"两直线平行，内错角相等"的性质解答.

例3如图5，已知 AB//CD ∠B=38∘ ∠D=72∘ ，则 ∠BED= 。（剩余6217字）