巧添中线，妙解三角形问题

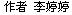
打开文本图片集

在有关三角形的问题中，“中点"既是常见考点，也是破解复杂问题的关键线索之一，当我们在解题时遇到中点时，添加中线往往能为我们打开一扇通往答案的“大门”.中线不仅能平分线段，还能构造全等、转化图形，搭建连接已知与未知的“桥梁”.本文将通过几个典型例题，探讨如何巧添中线，以便利用中线的性质妙解三角形问题

一、巧添三角形的中线，利用线段之间的比例关系解题

当任意一个三角形的一边上有中点时，可连接中点与顶点构成中线，则中线将对应边平分，分割的比例为1：1.若三角形的三条中线相交，则交点为重心，且重心将每条中线分割的比例为2：1.利用这些线段之间的比例关系可以解答线段的长度问题以及三角形的面积问题.

例1如图1， G 是 ΔABC 的重心，则SΔABG：SΔACG：SΔBCG 的比值为

图1

解析：如图1，取 BC 的中点 D ，连接 GD 因为 G 点为 ΔABC 的重心，所以A， G，D 三点共线，

即 AD 是 BC 边上的中线.

由于 ΔABD ， ΔACD 等底等高，所以

因为 G 点为 ΔABC 的重心，

所以 AG：GD=2：1

所以 ，

由于 ΔABG ， ΔABD 的高相等，所以SABG

同理可证 业所以 SΔABG SΔACG . SΔBCG=1：1：1

评注：本题中，取一边中点，连接中线，由于中线将对应边平分，故中线将整个三角形的面积分成相等的两部分，而重心又将三角形的中线分割为2：1，所以把以中线为底边的三角形的面积分为2：1的两部分.由线段之间的比例关系能很快推导出各个三角形的面积比例关系.

二、巧添三角形的中线，利用“三线合一”的性质解题

在遇到与等腰三角形有关的问题时，若遇到底边有中点，常作底边上的中线.由于等腰三角形底边上的中线也是底边上的高和顶角平分线，因此利用等腰三角形“三线合一”的性质，能同时得到线段相等或垂直的关系，以及角相等的结论，再结合三角形的其他知识即可求解线段或角之间的数量关系问题。（剩余1140字）