基于有限质点法和空间分割技术的平面固体接触碰撞行为分析

打开文本图片集

中图分类号034；TU31 文献标识码A

0 引言

接触问题分析广泛应用于汽车碰撞分析、机械零部件磨损、土木结构变形与破坏等场景.其研究不仅有助于提高工程设计的精确性和可靠性，也对保障结构安全性和优化产品性能具有重要作用.然而，接触问题的研究面临诸多挑战，尤其是涉及多重非线性耦合，包括材料非线性、几何非线性和接触界面的非线性，这些非线性相互作用增加了问题求解的复杂性.

在求解接触问题时，荷载增量选择和时间步长的设定对收敛性提出了较高要求，尤其是在动力学分析中，接触界面的变形较大时，收敛难度更大.此外，数值稳定性和计算效率也是接触问题中的重要难点.过小的时间步长会增加计算量，而过大的步长则可能导致数值不稳定，影响最终结果的准确性.如何在保证精度的同时提高计算效率，避免过度迭代，是当前研究的关键2.接触侦测是固体碰撞数值分析的关键步骤，常用的方法包括基于网格划分的接触搜索算法、基于空间分割的接触侦测方法、基于遗传算法优化的接触侦测方法等.基于空间分割的接触侦测方法由于其实施简单、效率高，在接触侦测中使用广泛.

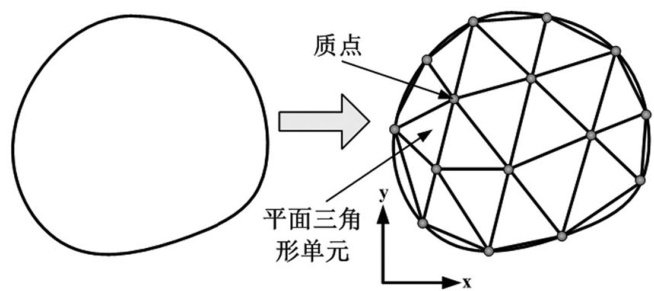
基于向量式结构与固体力学，罗尧治等提出了用于结构复杂行为分析的有限质点法（Finite ParticleMethod，FPM）[4-7]，该方法是一种无网格方法.该方法在求解接触问题时，有较大的优势.主要表现在，FPM采用虚拟运动进行单元内力求解，计算非线性问题不需组集刚度矩阵，无需迭代求解8-9，大大简化了接触非线性问题的求解流程；FPM途径单元简化了变形描述，使得接触问题不在本质上增加求解困难，仅需要在途径单元间进行接触侦测和接触力求解，也无需预知和预设接触面；FPM分析域的质点满足牛顿第二定律，质点不受初始网格限制，容易增加和删除，对不连续行为（断裂、接触等）处理简便，而有限单元法受初始网格限制，对不连续行为需进行特殊处理。（剩余12064字）