以一道高考题为切入点分析一类力学问题

打开文本图片集

考试是考生在规定时间内独立解题的一种活动，因此在每届高三二摸或二模后我都要安排课堂教学时间让学生完成这样的学习任务：以某一题目或某一物理模型为抓手，多角度切入知识点、能力点，在同学与同学、同学与老师间互动中，达到复习、巩固知识和提高技能的目的，同时也训练了学生发散式思维.现从2023年广东高考物理卷第8题入手、多维度切入，以打开学生思维的阀门，以点带面达到复习巩固的效果.

14圆弧滑道特点：圆弧最高点的切线竖直，最低点的切线水平，与水平轨道平滑相接．

一、原题考了些什么

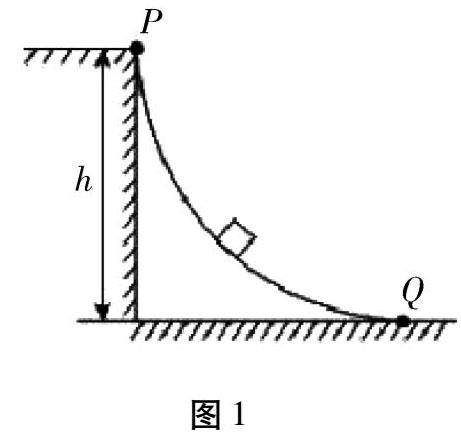
2023年广东高考物理卷第8题：（多选题）人们用滑道从高处向低处运送货物.如图1所示，可看作质点的货物从14圆弧滑道顶端p点静止释放，沿滑道运动到圆弧末端Q点时速度大小为6m/s .已知货物质量为20kg，滑道高度 h为4m，且过Q点的切线水平，重力加速度取10m/s2.关于货物从 P点运动到 Q点的过程，下列说法正确的有（  ）

A.重力做的功为360J

B.克服阻力做的功为440J

C.经过Q点时向心加速度大小为9m/s2

D.经过Q点时对轨道的压力大小为380 N

1.原题（答案为BCD）考查了：

A、B选项考查了功，C选项考查了向心加速度，D选项考查了牛顿第二定律等内容．

2.原题的物理情景不变，改变选择项，还可以考查那些知识点？

下列说法正确的有（答案为ABCDE）

A.货物发生的位移为42m，方向由P指向Q （位移矢量）

B.货物走过的路程为2πm （路程标量）

C.重力的功率先增大后减小（瞬时功率）

D.动量的变化量为120kg·m/s，方向向上（动量的变化量）

E.货物先失重后超重（失重与超重）

二、14圆弧滑道是一个固定物，圆弧滑道可以光滑也可以不光滑，以滑道为载体立意命题

1.引入一种相关物理运动，与原题物理运动对比考查相关知识．

【例1】 用一条材料和粗糙程度与圆弧滑道一样的直线滑道连接PQ，如图2所示，货物从P点沿直线滑道运动到Q点时的速度（  ）

A.等于6m/s

B.大于6m/s

C.小于6m/s

D.无法确定

【提示】圆弧轨道上货物克服摩擦力做功大于直线轨道上克服摩擦力做功，根据动能定理可得答案．

【答案】B

【例2】 如图3所示，竖直平面内有一半径为R的四分之一圆轨道与水平轨道相切于最低点B.一质量为m的小物块从轨道最高点A由静止滑下，沿轨道运动至C处停下，B、C两点间的距离为R，小物块与圆轨道及水平轨道之间的动摩擦因数相同.现用始终沿轨道切线方向的力推动物块，使物块缓慢由C处重返A处，重力加速度为g，设推力做的功至少为 W，则（  ）

A.W=mgR   B.mgR<W<2mgR

C.W=2mgR   D.W >2mgR

【解析】 设物块克服AB段摩擦力做功Wf，物块从A到C过程，根据动能定理得mgR-μmgR-Wf=0，解得Wf=mgR-μmgR，从C到A过程，物块克服BA段摩擦力做功W'f，根据动能定理得W-mgR-μmgR-W'f=0，解得W=mgR+μmgR+W'f，显然W >mgR，物块从A到B做圆周运动，根据向心力知识可知物块受到的支持力比缓慢运动时大，所以克服摩擦力做功Wf>W'f，可得W<2mgR，综上所述mgR<W<2mgR，故选B．

【答案】B

2.设计相关运动，使物理问题围绕14圆轨道呈现出来．

（1）巧用14圆轨道最低端的水平切线，与平抛运动结合．

【例3】 如图4所示，两半径皆为R的14圆轨道装置竖直固定.A、B为AB弧的最高点和最低点，圆心为O'，CD弧的圆心为O，B、O、C在同一水平线上，BO间距离为d（ d < R ）.游戏选手在O'圆轨道上某一位置释放小球，小球砸在圆O轨道上还能弹回到B点又沿圆O'轨道回到释放点，选手立刻收回小球即为游戏成功.某次有一选手把小球从某一位置释放，忽略空气阻力，小球可视为质点，重力加速度为g.小球与圆形轨道发生弹性碰撞，该选手要想游戏成功，小球应从多高位置释放.

【解析】 设小球过B点的速度为υ0，以υ0的初速度作平抛运动，以υ的速度与CD轨道发生弹性碰撞，反向延长线必过圆心O，由平抛运动规律得 x=2d，x=υ0t．

由几何关系y=R2-d2，又y=12gt2

解得υ0=d2gR2-d2 .

设小球在圆轨道上（或A的正上方）以与B点相距h高的位置释放，由机械能守恒得 mgh=12mυ20

解得h=d2R2-d2 .

（2）巧用14圆轨道最高端的竖直切线，与竖直上抛运动结合.

【例4】 如图5所示，abc是竖直面内的光滑固定轨道，ab水平，长度为2R；bc是半径为R的四分之一圆弧，与ab相切于b点.一质量为m的小球，始终受到与重力大小相等的水平外力的作用，自a点处从静止开始向左运动。（剩余2086字）