两个一次联手 巧解生活难题

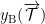
打开文本图片集

一元一次方程和一元一次不等式是初中数学的重点内容，中考中常设置具体情境，考查利用二者做决策的问题，下面举例介绍，

例某社区活动中心为鼓励居民加强体育锻炼，准备购买10副某种品牌的羽毛球拍，每副球拍配 x（x⩾2） 个羽毛球，供社区居民免费借用.该社区附近A，B两家超市都有这种品牌的羽毛球拍和羽毛球出售，且每副球拍的标价均为30元，每个羽毛球的标价均为3元，目前两家超市同时在做促销活动：

A超市：所有商品均打九折（按标价的 90% ）销售.

B超市：买一副羽毛球拍送2个羽毛球.

设在A超市购买羽毛球拍和羽毛球的费用为 yA （元），在B超市购买羽毛球拍和羽毛球的费用为 ．请解答下列问题.

（1）分别写出 yA，yB 与 x 之间的关系式；

（2）若该活动中心只在一家超市购买，你认为在哪家超市购买更划算？

（3）若每副球拍配15个羽毛球，请你帮助该活动中心设计出最省钱的购买方案，

分析：（1）根据购买费用 Σ=Σ 单价 × 购买数量，即可表示出 yA，yB 的解析式；（2）根据yA，yB 的解析式结合一元一次不等式，可分别求出购买划算的方案；（3）分两种情况进行讨论，计算求出需要的费用，再进行比较即可求出结论.

解：（1）由题意，得 yA=（10×30+3×10x）×0.9=27x+270（x⩾2） （204号 yB=10×30+3（10x-20）=30x+240（x⩾2）.

（2）当 yA=yB 时， 27x+270=30x+240 ，解得 x=10 当 yA>yB 时， 27x+270>30x+240 ，解得 x<10 当 时， 27x+270<30x+240 ，解得 x>10

因此，当 2⩽x<10 时到B超市购买划算；当 x=10 时在两家超市购买一样划算； 当 x>10 时在A超市购买划算.

（3）由题意知 x=15>10 ，若选择A超市，则费用为 yA=27×15+270=675 （元）.

若先选择B超市购买10副羽毛球拍，送20个羽毛球，然后在A超市购买剩下的羽毛球，

则费用为 10×30+（10×15-20）×3×0.9=651（ （元）

： ⋅651<675 ，：最佳方案是先在B超市购买10副羽毛球拍，然后在A超市购买130个羽毛球，

点评：一元一次不等式与一次函数的实际应用综合问题是中考的热点题型，此类问题虽出题方式和出题背景多变，但解题思路相对固定：关键是找出题干中的等量关系和不等量关系，根据问题写出计算结果或表达式，而后对其进行分析.

分层作业

难度系数： 解题时间：18分钟

1.某公司计划购买若干台电脑，现从两家商场了解到同一种型号的电脑报价均为4000元，并且多买都有一定的优惠.各商场的优惠条件如下：

甲商场优惠条件：第一台按原价收费，其余的每台优惠 15% 。（剩余581字）