一类不连续Sturm-Liouville问题的特征值与特征函数零点估计

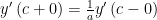
打开文本图片集

中图分类号：0175.9 文献标志码：A doi：10.12415/j.issn.1671-7872.24006

Esimation of Eigenvalues and Zeros of Eigenfunction for a Class of Discontinuous Sturm-Liouville Problems

ZHANG Yanxia²， ZHANG Zhiqiangʰ， LIU Yannian'， ZHU Zhongyang' （a. School ofMicroelectronics & Data Science; b.School ofComputer Science & Technology，Anhui University of Technology，Maanshan ， China）

Abstract： For discontinuous Sturm-Liouville problems （SLPs） with periodic boundary conditions， the asymptotic estimates of two linearly independent solutions were first derived based on the initial value theory of ordinary differential equations. Subsequently， the asymptotic form of eigenvalues for discontinuous SLPs was established by employing Gronwall's inequality，eigenvalue properties， and the asymptotic solution estimates.Finall， it was proved through the Prufer transformation that the eigenfunction corresponding to the n -th eigenvalue possessed exactly n zeros within the interval （0，c）∪（c，π） .This study provides important theoretical foundations for the precise calculation of eigenvalue indices and the oscilltory analysis of solutions for discontinuous SLPs.

Keywords： Sturm-Liouville problems； transmision conditions; eigenvalue;；periodic boundary condition;Prufer transform; gronwall inequality

文中研究由二阶微分方程（1）和周期边界条件（2），（3）及转移条件（4），（5）构成的不连续Sturm-Liouville问题（Sturm-Liouville problems，SLPs）。（剩余9005字）