“十字架模型”的特点及其在解答几何题中的应用

打开文本图片集

“十字架模型"是初中平面几何中一种结构清晰、用途广泛的典型模型.它由正方形、矩形等几何图形内两条相互垂直的线段组成.下面通过探究该模型的基本性质和几何特征，推导出该模型的核心性质与常用结论，然后结合典型例题分析该模型在解题中的应用方法，希望能帮助同学们在面对这类问题时，能够迅速识别并恰当地搭建“十字架模型”，并借助相关结论高效解题

一、正方形中的"十字架模型”及其应用

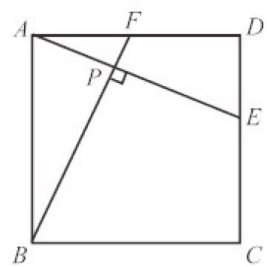
在正方形中，分别连接正方形的顶点与对边的点，所得两条线段若垂直，构成“十字架模型”，则线段长度相等.如图1，在正方形ABCD中，分别连接顶点 A，B 与对边上的点 Ei F ，若 AE⊥BF ，则 ΔADE≅ΔBAF，AE=BF

简证：若 AE⊥BF ，则 ∠ABP+∠BAP=90∘ 而 ∠DAE+∠BAP=90∘ ，所以 ∠DAE=∠ABP

再利用正方形的性质得到 DA=AB ∠ADE=∠BAF 0

则 ΔADE≅ΔBAF（ASA），AE=BF. （204号

图2是模型1的变式，若 EF⊥GH ，通过线段平移可以推出 EF=GH. 在有关正方形的折叠与求几何最值等问题中常出现"十字架模型”，在解题时可以直接利用模型的结论证明三角形全等，得到一些线段、角的相等关系，进而简化几何问题的分析过程。（剩余1311字）