直线上负长度增长率系统

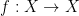
打开文本图片集

Dynamics on line with negative growth rate of length

DING Mingzhou,HE Baolin*

(Mathematicsand Science College,Shanghai Normal University,Shanghai 2Oo234,China)

Abstract:In order to study the entropy continuity of differential homeomorphic systems on a straight line,the second author ofthis paper first introduces the length growth rate of differential homeomorphic systems ona straight line.This paper mainly proves that for the orientation-preserving diffrential homeomorphism on a straight line, the system has a negative length growth rate if and only if the system has an unique fixed point, which is attracting. For general differential homeomorphic systems on a straight line, we only obtain partial results.

Keywords:differential homeomorphism；length growth rate；orientation-preserving；orientation-reserving; attracting fixed point

0引言

在文献[1]中，为了研究直线上微分同胚系统的熵的连续性，首次引入了直线上同胚系统的长度增长率．由于负长度增长率不提供熵，该文没有刻画此类系统．基于[1]中长度增长率的定义，本文给出了一个长度增长率的估计，并刻画了直线上具有负长度增长率的微分同胚系统．若 R 上微分同胚是单增的，则称为保向的.

定理1 (1)设 f 为 R 上微分同胚且 l(f)′(p)|′(p)|

定理2设 f 为 R 上保向微分同胚，则 l(f)′(p)

显然，定理1可直接得到定理2.定理2完全刻画了直线上具有负长度增长率的保向微分同胚．下面，给出本文需要的基本定义.

定义1设连续映射 f:R⟶R, 称 p 为 f 的不动点，若 f(p)=p 不动点 p 称为吸引不动点，若存 在 p 的邻域 I, 使得对任意 :x∈I,limn⟶+∞fn(x)=p. （2

不难验证，若 |f′(p)|

定义 2[3] 设 X 为度量空间， 同胚．令 K⊂X 为紧子集．设 ε>0; 一个子集 E⊂K 被称为 K 的 (n,ε)- 分离集，若对任意 x,y∈E, 存在

i∈{0,1,⋯,n-1},

满足 d(fix,fiy)>ε. 令

式中： #E 表示 E 中元素个数．称

为 f 在 K 上的拓扑熵． f 的拓扑熵定义为

h(f)=supK⊂Xh(f,K),

其中 K 取遍 X 的所有紧子集

下面长度增长率的定义是[1]引入的，刻画了长度增长率与熵的紧密联系，

定义3若 I 为有界区间，令 f 在 I 上的长度增长率为

对一般区间 令 f 在 J 上的长度增长率为

l(f,J)=supI⊂Jl(f,J),

式中： I 取遍 J 的有界子区间．特别地， l(f,R) 简记为 l(f), 称为 f 的长度增长率

定义直线上保向和反向同胚．显然，直线上同胚分成保向与反向两类动力系统．WALTERS[3]证明了长度增长率的基本迭代性质.基于这个性质，可以把直线上所有系统转化为保向(严格增)同胚系统

引理1对 R 上任意微分同胚与任意正整数 k, 有 l(fk)=kl(f) 由于本文方法需要导数估计长度增长率，不能刻画一般同胚系统的长度增长率，

1定理的证明

本章将给出长度增长率的估计，并完成定理的证明，即直线上保向微分同胚系统具有负长度增长率，当且仅当它具有唯一不动点，且该不动点为吸引的.

引理2设 f 为 R 上同胚，有界区间 I⊂R, 且存在正整数 N 以及 0

则 特别地，若 {(fn+1） =+∞,则l（f）=+∞.

证明由于对任意 n⩾N 有：

则

由上确界定义知：

再由 l(f,I) 的定义可得：

特别地，若 +）=+∞,则l(f,I)=+∞.由l(f）的定义可得l(f)=+∞.

下面证明定理1.

引理3设 f(x) 为 R 上微分同胚， p∈R, 且对任意 x∈R, 有 fn(x)p, 则

证明由于 f 连续可导，则对任意 ε>0 ，存在正数 δ, 使得对任意 x∈(p-δ,p+δ)

|f′(x)-f′(p)|

设 I=[a,b] 为 R 上有界区间，由 p 的整体吸引性知，存在正整数 N, 使得当 n>N 时，对任意 x∈I 都有：

p-δn(x)

从而对任意 x∈fn(I). 有 |f′(x)-f′(p)|

由Lagrange中值定理知，存在 ξn∈[fn(a),fn(b)] 使得：

即

由对任意 x∈fn(I), 有 |f′(x)-f′(p)|′(ξn)∈[f′(p)-ε,f′(p)+ε]. ，则对任意 n>N 有：

从而由引理2知：

故

再由 l(f) 的定义可知，取遍 R 上有限区间 I,

综上所述，

下面证明定理2.

证明先证充分性．由于 f 有唯一不动点 p 且 f′(p)0 。（剩余5861字）