路的幂图的奇色数和正常无冲突色数

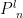
打开文本图片集

中图分类号：0157.5 文献标志码：A

Odd Coloring and Proper Conflict-free Coloring of Power Graph of Path

WANG Tai-shan 1 ，MENG Jia-wei²，CHEN Chun-mei 1 ，WANG Shi-jie 1 （1.Mathematics Section，Department of Basic Education， Rocket Force University of Engineering，Xi'an 71Oo25，China; 2.School of Aerospace Information，Aerospace Engineering University，Beijing lO1416，China）

Abstract：In this paper，we analyze the structure of the power graph of path. The lower bound of the odd chromatic number of the power graph of path is obtained using contradiction，and the upper bound of the proper conflict-free chromatic number of the power graph of path is obtained by constructing the specific coloring. Finally，based on the relationship between the two coloring，we determine the odd chromatic number and proper conflict-free chromatic number of power graph of path. Furthermore，a smaler upper bound of the odd chromatic number and the proper conflict-free chromatic number of some planar graphs is obtained. It enriches the theories of odd staining and normal conflict-free staining of graphs， providing theoretical guidance for practical applications.

Key words：power graph;odd coloring;proper conflict-free coloring

0 引言

2022年，PETRUSEVSKI M 和 SKREK-OVSKI R[1] 提出了奇染色的概念，并证明了平面图的奇色数的上界是9.文献[2中给出了该结论的一个更简单的证明，并给出了路、树、圈和超立方体等经典图类的奇色数．2023年，PETRJ等[3将平面图奇色数的上界降到了8．关于图的奇染色的更多研究结果可见文献［4-8].

对奇染色的条件进一步限制，CAROY等[9]提出了正常无冲突染色的概念，给出了树、圈和超立方体的正常无冲突色数，并证明了平面图的正常无冲突色数的上界在6到8之间.关于图的正常无冲突染色的更多研究结果可见文献[10-13].

本文针对一般的路的幂图，研究其奇染色和正常无冲突染色，利用结构分析法、反证法和构造具体染色法，结合两类染色之间的关系，完全确定了一般的路的幂图的奇色数和正常无冲突色数，得到了部分平面图的奇色数和正常无冲突色数的更小的上界.

1预备知识

本文所讨论的图都是简单无向图.设简单图G=（V（G），E（G）） ，任取点 υ∈V（G） ，用d（v） 和 Δ（G） 分别表示点 v 的度和图 G 的最大度.文中未加叙述的术语、记号参见文献[14].

定义 1[1] （204号 如果图 G 的一个 k- 染色 φ 满足：对任意顶点 υ ，存在 c∈{0，1，2，…，k-1} ，使得|φ-1（c）∩N（v）| 是一个奇数，则称 φ 是 G 的一个奇 k- 染色.特别地，称 Ψc 为点 υ 的奇色．图 G 的奇色数是使 G 有一个奇 k- 染色的最小的 k ，记作X。（剩余4762字）