高阶Maggi方程的Birkhoff化及其辛算法

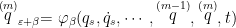
打开文本图片集

中图分类号：0316

文献标志码：A

Birkhoffization of Higher-Order Maggi Equation and Its Symplectic Algorithm

Xue BingXie Jiafang†Zhang Kexin （College of Science，North China University of Technology，Beijing 1Ool44，China）

Abstract For the high-order Maggi equation of nonholonomic systems，when it meets certain conditions，the Maggi equation can be transformed into a Birkhofian system.By constructing the generating function，the system is investigated numerically using the symplectic geometric algorithm of the Birkhoffian system.Compared with the above-mentioned algorithm with the classical Runge-Kutta method， Birkhoffian symplectic scheme is very accurate in a long-term tracing.

Key wordsnonholonomic system， Maggi equation， Birkhoffian symplectic algorithm

引言

非完整系统是一类受到不可积微分约束的动力学系统[1]，广泛应用于场论、机电动力系统、控制理论、工程科学等领域2.20世纪80年代我国学者梅凤翔研究了带参数约束的一类可控系统[3]、变质量非完整约束系统.Maggi在1896年推广了拉格朗日第二类方程[4]，对线性非完整约束系统得到一类动力学方程，后人称为Maggi方程[5]，这些方程后来被推广到非线性非完整系统[6].Maggi方程是力学系统[各大运动方程的中间产物，对研究非完整系统的运动具有重要意义.

Birkhoff动力学理论是Hamilton动力学的自然推广，它是包括齐次Hamilton系统和非齐次Hamilton系统的更一般动力学理论，是最一般辛结构的局部实现，只有Birkhoff系统与一般辛几何结构之间才有一一对应关系.因此Birkhoff系统动力学[8的研究对于完善和深化分析力学的理论体系具有重要意义，尤其是对于非齐次Hamilton动力学系统的几何结构分析具有重要应用价值9.本文针对非完整系统高阶Maggi方程，在其满足一定条件下，将其进行Birkhoff化。（剩余5367字）